Zarz Ryz Finans R18W1

18. Zarządzanie ryzykiem cenowym w portfelu instrumentów pochodnych 571

podczas gdy inni używają określenia kappa\ W niniejszym przykładzie oraz w dalszej części książki będziemy posługiwać się nazwą vega (choć jest to marka samochodu, a nie grecka litera). Vega stanowi miarę zmiany wartości instrumentu finansowego, jaka zachodzi w związku ze zmianą zmienności stóp procentowych (czy innych cen pierwotnych).

Vega = A wartości waloru finansowego/Ao

Wśród instrumentów pochodnych - kontraktów forward i futures, swapów i opcji - tylko wartość opcji jest uzależniona od zmienności. Tak więc o ile współczynnik gamma charakteryzuje przede wszystkim opcje, o tyle vega odnosi się wyłącznie do tych instrumentów⁴.

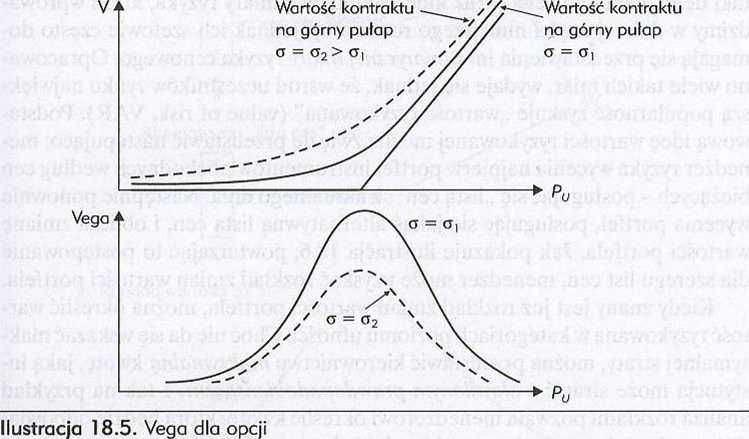
Ilustracja 18.5 przedstawia dwa profile wartości opcji: dla jednego z nich zmienność stóp procentowych wynosi a₍, a dla drugiego - c„ przy czym a, < a,.

•’ Zamieszanie jest tym większe, że w niektórych podręcznikach akademickich ten parametr ryzyka nazywany jest lambda.

^J Jak widzieliśmy we wcześniejszych rozdziałach tej książki, zmiany zmienności wpływają na wartość opcji, lecz nie zmieniają wartości kontraktów forward, futures ani swapów.

Zdarzają się jednak szczególne przypadki, kiedy można twierdzić, że również instrumenty finansowe inne niż opcje wykazują niezerową wartość vega. Załóżmy na przykład, że struktura czasowa stóp procentowych odpowiada procesowi Coxa-Ingersolla-Rossa (por. rozdz. 13, przyp. 8): krótkoterminowe stopy procentowe określają strukturę cen obligacji. Jeśli w takich warunkach wzrośnie zmienność stóp krótkoterminowych bez zmiany ich poziomu, to instrumenty finansowe charakteryzujące się niezerowym współczynnikiem gamma będą również miały niezerową vegę.