0262

264

XI. Szeregi nieskończone o wyrazach stałych

383. Przekształcenie Abela. Często trzeba rozpatrywać sumy iloczynów postaci

W

(9)    S = '£cc_ip_i = ct₁p₁+ct₂p₂+ ... +<x_np„.

i=l

W wielu przypadkach okazuje się przy tym pożyteczne następujące przekształcenie podane przez Abela.

Wprowadzimy sumy

^1 ⁼ Pl> -®2 ⁼ Pl+p2> B₃ — Pl 4“ Pz 4" Pi)    • ••> B_m = P1+P1+ ••• +Pm •

Wyrażając czynniki /J₍ przez te sumy

Pi — Bi* Pz = B₂ — B_l, p₃ = B₃-B₂,    ..., P_m = B_m—B_m~_t,

możemy sumę S napisać w postaci

S = a_lB₁+a₂(B₂-B₁) + x₃(B₃-B₂) + ... +x_m(B_m-B_m-₁) .

Jeżeli otworzymy nawiasy i zgrupujemy inaczej wyrazy, to otrzymamy ostateczny wzór

m

(10)    S = ^<x_tPi = (a₁-a₂)B₁+(a₂-a₃)B₂+ ... +(*,„-!-a,„) B_m-_l+x_m B_m =

i-1 m-l

= '^(a_i-x_l+1)B_i + x_m B_m^(l) .

i~l

Jeżeli napiszemy ją w postaci

m    im-i

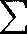
*tPi =    ^(at+t-a^Bi,

i-ł

to widać, że wzór ten dla sum skończonych jest analogonem wzoru na całkowanie przez części dla całek — różniczka jest tu zastąpiona różnicą, a całka sumą.

Opierając się na wzorze (10) wyprowadzimy następujące oszacowanie dla sum tego typu.

Lemat. Jeżeli czynniki a, nie rosną (albo nie maleją), a sumy B_t są wszystkie ograniczone co do wartości bezwzględnej liczbą L,

(i = 1, 2, ..., m)

to

|S| =

Rzeczywiście, ponieważ wszystkie różnice w (10) mają ten sam znak, więc jest

Ml—1

|S| <^|a,-a₍₊₁| L+\x_m\L = 1(1*1-aj+ |aj) <L(|a,|+2 |aj) .

(^l) W istocie posługiwaliśmy się takim przekształceniem w dowodzie drug iego twierdzenia o wartości średniej [306],