0342

344

XI. Szeregi nieskończone o wyrazach stałych

Jest od razu jasne, że rozpatrywana metoda sumacyjna jest liniowa. Regularność tej metody, wynika z następującego twierdzenia Abela:

Jeżeli szereg (A) jest zbieżny i ma sumę równą A (w zwykłym sensie), to szereg potęgowy (1 )jest dla 0 < x < 1 zbieżny i jego suma dąży do A, gdy x -¹■ 1 —0 (’).

Przede wszystkim jest jasne [379], że promień zbieżności szeregu (1) jest nie mniejszy od I, tak że dla 0 < x < 1 szereg (1) jest rzeczywiście zbieżny. Wiemy już, że zachodzi tożsamość

00    00

^a„x" = (l-x)^A_Bx¹,

n=0    n¹0

gdzie A_n = a₀+a_t + ... +a_n [patrz 385, 6) lub 390, 4)]. Odejmijmy tę tożsamość stronami od oczywistej tożsamości

00

A = (1— x)^ Axⁿ .

Ii-O

Po wprowadzeniu oznaczenia A — A„ = a„ otrzymamy tożsamość

W    A ~ ^ a„ x" = (1 —x) ^ ot_B x".

n=0    n-0

Ponieważ a_B -» 0, przeto do dowolnie danej liczby e > 0 można znaleźć takie N, że |oc„| < c -jb, jeśli tylko n > N.

Rozbijemy sumę szeregu po prawej stronie wzoru (4) na dwie sumy

N    co

u-oy² i (i-¹)

E

B=0    n=N+l

Druga suma daje się od razu oszacować niezależnie od x:

oc„ x

n~N+t

ir=N+l

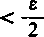
oo.

•(1—x) ^ X" »“W+1

pierwsza zaś dąży do 0, gdy x -¹ 1, i dla x dostatecznie bliskich 1 będzie

<_Te,

(l-x)^a_B

więc ostatecznie

00

co należało udowodnić.

^A~

n=0

1

Twierdzenie to udowodnił Abel w swych badaniach dotyczących teorii szeregu dwuniiennego (powrócimy jeszcze do niej w ustępie 437, 6°). Nie ulega wątpliwości, że właśnie to twierdzenie naprowadziło na ogoine sformułowanie metody sumowania uogólnionego, którą Poisson zastosował tylko w szczególnym przypadku. W związku z tym metodę tę nazywają często metodą Abela, chociaż idea sumowania

2

szeregów rozbieżnych była samemu Abeiowi w najwyższym stopniu obcą. W dalszym ciągu mówiąc o tej metodzie będziemy ją nazywali metodą Poissona-Abela.