0310

312

XI. Szeregi nieskończone o wyrazach stałych

skąd na mocy 8° wynika, że nasz iloczyn jest bezwzględnie zbieżny. Zdefiniowana przez ten iloczyn funkcja F(x) jest po funkcjach elementarnych jedną z najważniejszych funkcji rozpatrywanych w analizie matematycznej. Dalej, w rozdziale XIV, § 5, podamv inną definicję tej funkcji i zbadamy głębiej jej własności.

Ponieważ n-ty iloczyn częściowy ma postać

(«+!)*

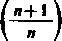
x(x+\)(x+2) ... (x+n) ’

JK

n! tf

można także przyjąć

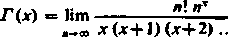
x (*+1) (at+2) ... (x+n)

(14)

Pisząc analogiczny wzór dla .T(jr+1) łatwo zauważyć, że

Otrzymujemy prosty i ważny związek

r(^+l) = xT(x).

(15)

Jeśli podstawimy za x liczbę naturalną m, otrzymamy wzór redukcyjny

r(m+l) = m■ r(m),

a że /'(l) = 1, jak łatwo sprawdzić, to otrzymujemy stąd

/'(m+l) -- ml

Jeszcze jeden ważny wzór dla funkcji r (x) otrzymamy, jeśli pomnożymy stronami równości

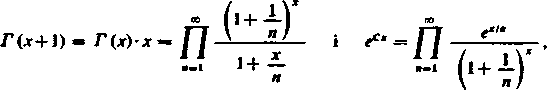
z których pierwsza wynika z (13) i (15), a druga wyprowadza się łatwo z 400, 6). Otrzymujemy

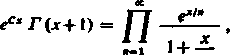
n

czyli

00

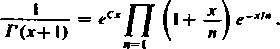
(16)

Jest to wzór Weierstrassa.

11) Przytoczymy słynny przykład przekształcenia iloczynu nieskończonego w szereg, który także należy do Eulera. Jeżeli ponumerujemy liczby pierwsze w kolejności ich wzrastania

Pi =2, pi = 3, Pi = 5,

to dla jt>1 zachodzi tożsamość