0298

300

XI. Szeregi nieskończone o wyrazach stałych

Uwaga. Nie należy jednak myśleć, że graniczny punkt A/*, o którym mówiliśmy przed chwilą, koniecznie pokrywa się z punktem rozgraniczającym M₀ samej osi x. Punkt M₀ może leżeć na prawo od M*, a nawet w nieskończoności. Możliwość ta nie powinna czytelnika dziwić, bo lemat i oparte na nim rozumowania dotyczą tylko punktów spoza osi współrzędnych.

Uzupełnimy teraz krzywą skonstruowaną w pierwszej ćwiartce krzywymi symetrycznymi do niej względem jednej i drugiej osi współrzędnych i leżącymi w pozostałych ćwiartkach. W ten sposób otrzymamy całą krzywą rozgraniczającą, która określa interesujący nas obszar zbieżności ^clfl. W części płaszczyzny leżącej wewnątrz tej krzywej szereg (14) jest zbieżny i to bezwzględnie, w zewnętrznej części płaszczyzny szereg jest rozbieżny (^ł), a w punktach samej krzywej szereg może być albo zbieżny, albo rozbieżny.

397. Przykłady. 1) Obszar zbieżności ^cWf szeregu

00

E

l,k-0

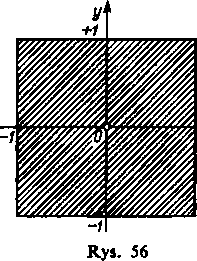
sprowadza się, jak widzieliśmy w 395, 8), do otwartego prostokąta (— 1,1; — 1, 1) (rys. 56); w tym obsza-. • ^{1 1}

rze suma szeregu jest równa -----.

1—ar    1 —y

2) Obszar zbieżności analogicznego szeregu

00

E

i.t-i

gdzie wskaźniki przebiegają wartości zaczynające się od 1, będzie się składał z tego samego prostokąta, ale z dołączeniem obydwu osi współrzędnych. W tym przypadku, chociaż rozgraniczający punkt M_e, o którym była mowa wyżej, dąży przy 0 -*• 0 do granicznego punktu M* (1, 0) na osi x, szereg jest mimo o zbieżny na całej osi (patrz uwaga).

+1 x

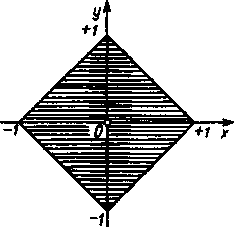
Rys. 57

3) Szereg

00 00 00 v = V—• vz

Zj i! k\    Zj i! ' Zj k\

jest oczywiście bezwzględnie zbieżny w całej płaszczyźnie.

(‘) Jeżeli nie brać pod uwagę osi współrzędnych, wzdłuż których, jak wspomnieliśmy, szereg może być zbieżny także i na zewnątrz tej krzywej.