0276

278

XI. Szeregi nieskończone o wyrazach stałych

Przy praktycznym mnożeniu szeregów najczęściej jest wygodnie ustawiać iloczyny (7) po przekątnych, jak w (8); łączy się przy tym wyrazy leżące na jednej przekątnej

(13)    A.B “    "i" ^2^2 "1"    •••

W tej właśnie postaci przedstawił Cauchy po raz pierwszy iloczyn dwóch szeregów. Tak napisany szereg będziemy dalej nazywali iloczynem szeregów (A) i (B) w postaci Cauchy'ego, lub krócej, iloczynem Cauchy'ego.

Pomnóżmy, na przykład, dwa szeregi potęgowe

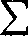
a—O

oo

ajc" = fl₀+aix+a2*¹+ ••• +tfnX"+ ....

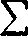
bjx!” = b₀ + biX+b₂x¹+ ... +b_mx^m+ ...,

«-0

przy czym x leży wewnątrz odpowiednich przedziałów zbieżności [379]. Wówczas łatwo zauważyć, że podany sposób mnożenia odpowiada redukcji wyrazów podobnych w iloczynie

OD    00

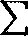
a_m z* • b_m «* a₀ b₀+(a_Q ój+Ui ó₀)*+(flo *2+fli t>i+ai *o)*¹ + —

a—0    a»—O

Tak więc iloczyn w postaci Cauchy’ego dwóch szeregów potęgowych daje bezpośrednio szereg potęgowy.

390. Przykłady. We wszystkich przykładach oprócz ostatniego bierzemy iloczyn szeregów w postaci Cauchy’ego.

1)    Mnożąc szereg

-i— = fy=i+*+**+... +*»+... (w<D

^l~^x to

przez siebie, otrzymujemy

oraz

(14)

£(-1)—¹

m

m

(W<1) daje następujący wynik:

V(-iy‘-ⁱH_lrx* = x- (i+y)*¹+ ... +(-«*-> (i+j+ ... + |-)*‘+

Zobaczymy niżej [403], że sumą szeregu (14) jest ln(l+x), ostatni szereg przedstawia zatem funkcję ln (1 +jc)

1

   Mnożenie szeregów

1

l+x