0316

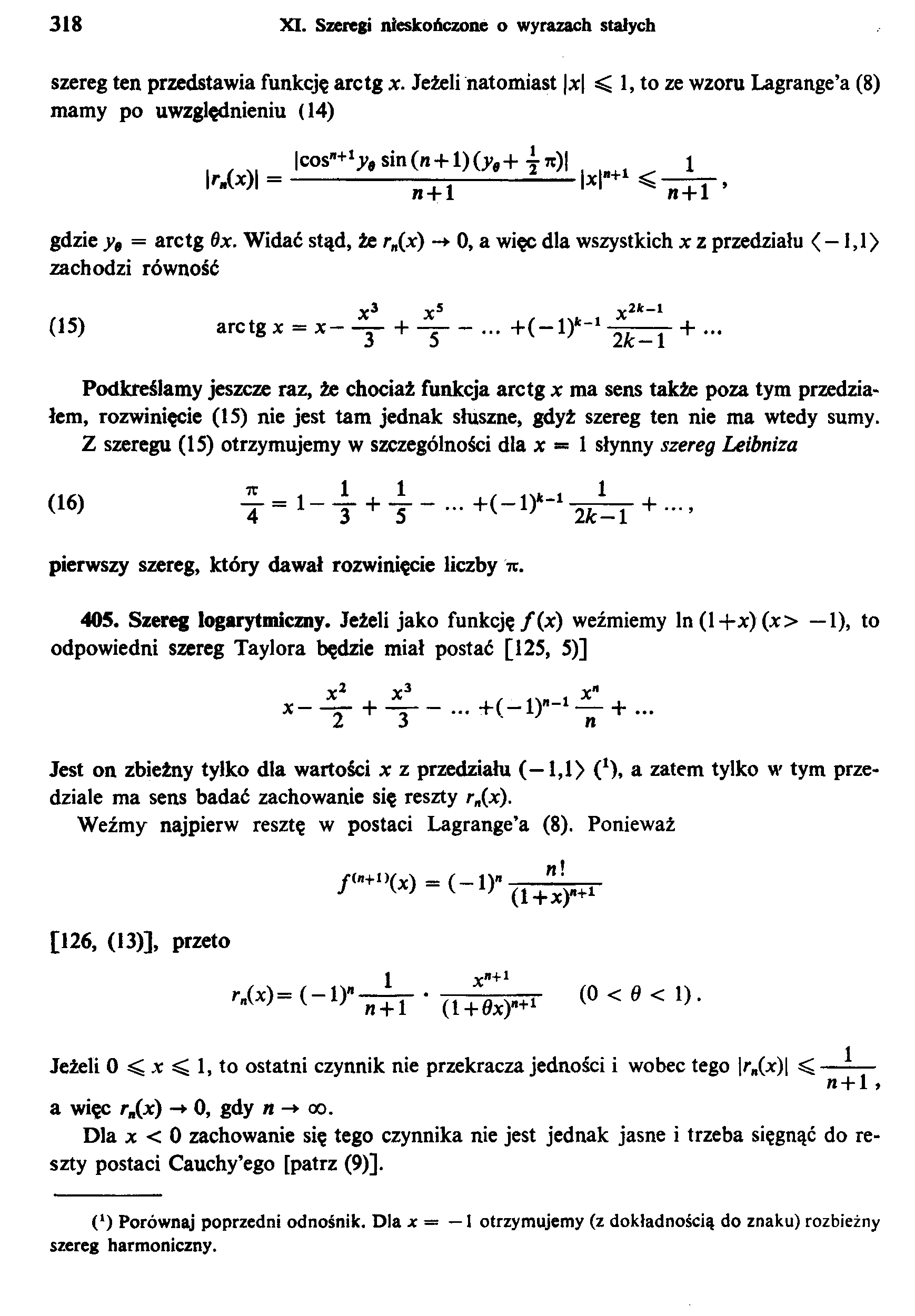
318

XI. Szeregi nieskończone o wyrazach stałych

szereg ten przedstawia funkcję arctg x. Jeżeli natomiast |x| < 1, to ze wzoru Lagrange’a (8) mamy po uwzględnieniu (14)

|cos'^,+1,y_# sin (n +1) (y„ + j tc)|

n + i

|x|"⁺¹ <

1

n + 1 ’

gdzie y_t = arctg 8x. Widać stąd, że r„(x) -* 0, a więc dla wszystkich x z przedziału < -1,1) zachodzi równość

(15)    arctg x = x —— ...    + ...

Podkreślamy jeszcze raz, że chociaż funkcja arctg x ma sens także poza tym przedziałem, rozwinięcie (15) nie jest tam jednak słuszne, gdyż szereg ten nie ma wtedy sumy. Z szeregu (15) otrzymujemy w szczególności dla x = 1 słynny szereg Leibniza

pierwszy szereg, który dawał rozwinięcie liczby tc.

405. Szereg logarytmiczny. Jeżeli jako funkcję/(x) weźmiemy ln(l-|-x)(x> —1), to odpowiedni szereg Taylora będzie miał postać [125, 5)]

x —

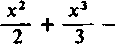
+(-l)"-¹—+ ...

Jest on zbieżny tylko dla wartości x z przedziału (—1,1) (*), a zatem tylko w tym przedziale ma sens badać zachowanie się reszty r_B(x).

Weźmy najpierw resztę w postaci Lagrange’a (8). Ponieważ

-<-')■ (nsk

[126, (13)], przeto

'■<*>-<-‘>■^•<1^ (0 < 0 < 1).

Jeżeli 0 < x < 1, to ostatni czynnik nie przekracza jedności i wobec tego |r„(x)| <—-—

n + 1,

a więc r„(x) -* 0, gdy n-* co.

Dla x < 0 zachowanie się tego czynnika nie jest jednak jasne i trzeba sięgnąć do reszty postaci Cauchy’ego [patrz (9)].

(‘) Porównaj poprzedni odnośnik. Dla x = — 1 otrzymujemy (z dokładnością do znaku) rozbieżny szereg harmoniczny.