0320

322

XI. Szeregi nieskończone o wyrazach stałych

Ponieważ

/^l"⁺¹⁾(x) = m (m —1) ... (m — n + l)(m — n)(l + x)^m-"^_1 ,

mamy

rM -    ₍₁ __v^

1-2* ... -n

Przegrupujemy czynniki i przedstawimy tę resztę w postaci

r„(x)

■[

(m — l)(m —2)... [(m-l)-n + l]

1-2-

xⁿJ • [mx (1 + 0x)‘

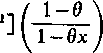
n

Pierwszy z tych trzech nawiasów przedstawia wyraz ogólny szeregu dwumiennego odpowiadającego wykładnikowi potęgi m— 1. Ponieważ szereg dwumienny jest dla |x| < 1 zbieżny przy każdym wykładniku, wyrażenie to dąży do zera, gdy n -* co. Co do dwóch pozostałych, to bezwzględna wartość drugiego jest zawarta między liczbami

|mx| (1 - IjcI)¹”-¹ i |mx| (t + |x|)^m-¹

niezależnymi od n, a trzeci — tak samo, jak w ustępie 405 — jest mniejszy od jedności. Tak więc r„(x) -* 0, tzn. dla |x| < 1 jest prawdziwe rozwinięcie

(1 +x)^m = 1 + hjx+

łączone również z nazwiskiem Newtona.

Nie rozpatrywaliśmy zagadnienia stosowalności tego rozwinięcia dla wartości x — ± 1. Łatwo dostrzec, że szereg dwumienny jest szczególnym przypadkiem szeregu hipergeometrycznego i powstaje z niego, gdy przyjmie się <x = — »»i, fi = y i gdy zastąpi się x przez —x. Wobec tego na podstawie tablicy z ustępu 402, 8) można łatwo zestawić podobną tabliczkę opisującą zachowanie się szeregu dwumiennego na końcach x = ± 1 jego przedziału zbieżności

	m> 0	bezwzględnie zbieżny
X = 1	0>m>—1	warunkowo zbieżny
	m< — 1	rozbieżny
X = -1	m> 0	bezwzględnie zbieżny
	m< 0	rozbieżny

Można udowodnić, że za każdym razem, kiedy szereg dwumienny jest zbieżny, suma jego jest równa (1 +x)“. Nie zatrzymujemy się tutaj na tym, aby uniknąć mozolnego badania reszty, gdyż wynik ten jest prostym wnioskiem z pewnego ogólnego twierdzenia, które zostanie niżej udowodnione [patrz 437, 6°].

Wypiszemy niektóre szczególne przypadki szeregu dwumiennego odpowiadające, na przykład, wykładnikom m — — I, -i, — ~ :

—i-= l-x+x^ł- ... +(-l)^,-x^,,+ ...    (-1 < x < 1)

1 +x

(zwykły szereg geometryczny), dalej

⁰³¹    ^ -¹⁺1'- T*‘⁺ T7*‘-    -

(-1 <x< 1)