0350

352

XI. Szeregi nieskończone o wyrazach stałych

Szereg	a> 00
(Q	y Cg = y. (ffo dt-ł-aMbo) ■-0 a-o

nazywa się iloczynem Cauchy’ego szeregów (A) i (B). Jeżeli dane szeregi są zbieżne i mają zwykle sumy A i B, to szereg (Q może być mimo to rozbieżny [przykład taki mieliśmy w ustępie 392].

Jednakże we wszystkich przypadkach szereg (Q jest samowolny metodą Poissona-Abela i to wlainie do sumy uogólnionej AB.

Rzeczywiście, dla 0<.*< 1 zarówno szereg (1) jak i szereg

00

2] ó« x" = óo+ói x+b₂ x²+ ... +ó. V+ ...

■-0

są bezwzględnie zbieżne [379], Oznaczmy ich sumy odpowiednio przez f(x) i g (z). Iloczyn tych szeregów, tzn. szereg

co    co

£ C.JC" =    (a₀ó.+<»ió.-i + ... +a_m-ibi+a_mb₀)jf,

■*0    ■—o

jest zbieżny na mocy klasycznego twierdzenia Cauchy’ego [389] i jego suma równa się /(x) • g (x). Suma ta dąźy do AB, gdy x -*■ 1 — O, bo jak widzieliśmy jest

lim /(x) = A i lim g(x) = B.

*-1-0    *-i-o

Uogólnioną sumą (w sensie Poissona-Abela) szeregu (Q jest więc rzeczywiście AB, co należało udowodnić.

Stąd wynika jako wniosek twierdzenie A bela o mnożeniu szeregów [392]. Z samego dowodu widać również, że teza twierdzenia pozostaje w mocy, jeżeli szeregi (A) i (B) nie są koniecznie zbieżne, ale tylko samowolne metodą Poissona-Abela odpowiednio do A i B.

Wobec tego, uwzględniając twierdzenie Frobeniusa [421], można także wypowiedzieć następujące twierdzenie:

Jeżeli szeregi (A), (B) i (C) są samowolne metodą Cesary i mają odpowiednio sumy uogólnione równe A, B, C, to musi byt C = AB.

Jako przykład rozpatrzymy podnoszenie do kwadratu szeregu

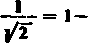
= 1-

J_ , _1 v3.

2    2-4

który to szereg powstaje z szeregu dwumiennego

1

»/T+7

+(—!)'

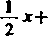
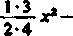
(2w-l)i! - , (2m)l!

gdy x = 1. Mnożąc powyższy szereg liczbowy przez siebie otrzymamy dobrze nam znany szereg

1 — 1 + 1 —1 + 1 —1+    C‘),

którego uogólniona suma, zarówno otrzymana metodą Poissona-Abela, jak i otrzymana metodą Cesary, jest równa -i = (1/|/2)¹.

(') Korzystamy tu z tożsamości liczbowej

(2ut—1)11 (2nt)l!

(2n-2m-1)1! _s j

(2n*2m)!l gdzie umawiamy się, że (—1)1! i 01! równają się jedności.