0354

356

XF. Szeregi nieskończone o wyrazach stałych

Można udowodnić, że k-krotne zastosowanie metody średnich arytmetycznych jest równoważne z za-stowaniem metody Cesary rzędu k, tzn. w obu wypadkach są sumowalne te same szeregi i do tych samych sum.

4) Metoda Borela. Dla szeregu (A) o sumach częściowych A„ tworzymy wyrażenie

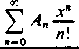
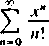
e

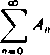
x“

n\

Jeżeli ostatni szereg jest zbieżny, chociażby dla dostatecznie dużych wartości x, i jego sumy dążą do granicy A, gdy x —¹■ cc, to liczbę tę nazywamy sumq uogólnioną w sensie Borela szeregu (A).

Udowodnimy regularność metody Borela. Załóżmy, że szereg (A) jest zbieżny i oznaczmy jego sumę przez A, a reszty A—A„ przez x„. Mamy dla dostatecznie dużych x

00

A — e~^x

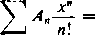
Hm 0

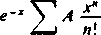
łl=«0

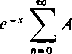
00

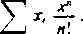
II mO

Weźmy dowolnie małą liczbę e>0. Istnieje takie N, że dla n>Njest |    Przedstawmy ostatnie wyra

żenie w postaci sumy

n    ot

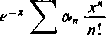
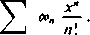
+ e~^x

n = 0    r-N + 1

Bezwględna wartość drugiego składnika jest mniejsza od-^-e dla każdego ,v, natomiast bezwzględna wartość pierwszego, będącego iloczynem e-^x przez wielomian, staje się mniejsza od dla dostatecznie dużych x. Tym samym jest wszystko udowodnione (').

5) Metoda Eulera. Dla szeregu

g(-UV

fc-0

otrzymaliśmy w ustępie 413, wzór (7)

(20) £(-1)%= £(-1)-!^,

»-o    p-o

dający tzw. przekształcenie Eulera. Udowodniliśmy przy tym, że ze zbieżności szeregu po lewej stronie wynika zbieżność szeregu po prawej stronie i równość sum tych szeregów.

Jednakowoż także w przypadku rozbieżności pierwszego szeregu może się okazać, że drugi szereg jest zbieżny. W takim przypadku Euler przypisywał sumę tego drugiego szeregu jako sumę uogólnioną pierwszemu. Na tym polega właściwie metoda sumowania Eulera. Podana przed chwilą uwaga gwarantuje regularność tej metody.

Jeśli napiszemy rozpatrywany szereg w zwykłej postaci (A) nie wydzielając znaków + i —, i uwzględnimy wzór (4) z ustępu 413 na różnicę rzędu p, to możemy powiedzieć, że w metodzie Eulera za sumę uogólnioną szeregu (A) przyjmujemy zwykłą sumę szeregu

2-+

s-

o ile ten ostatni jest zbieżny.

1

Czytelnik zauważy analogię między tym dowodem a dowodem twierdzenia Abela [418] i innych twierdzeń.