0410

412
XII. Ciągi i szeregi funkcyjne
(15) S(x+y) = S(x)-C(y)+C(x)S(y), prawdziwe dla wszystkich wartości x i y.
Kontynuujemy badanie własności funkcji C (jc) i S (jc). Zastępując x przez — x otrzymamy od razu, że C (jc) jest funkcją parzystą, a 5 (jc) — nieparzystą:
C(-x) = C(jc), 5(-x) = -S(jc) ,
Przyjmując jc = 0 otrzymujemy
C(0) = 1, 5(0) = 0.
Jeśli przy dowolnym x podstawimy teraz w (14) y = — jc, to uwzględniając wyprowadzone przed chwilą równości otrzymamy zależność algebraiczną wiążącą obie funkcje
(16) C2(jc)+52(jc) = 1 .
Łatwo też otrzymać wzory dla podwojonego i połówkowego argumentu.
Z twierdzeń 2° z ustępu 437 i 9° z ustępu 438 wnosimy, że obie funkcje C(jc) i 5 (jc) są nie tylko ciągłe, ale mają też ciągle pochodne wszystkich rzędów. W szczególności, stosując do tych szeregów określających nasze funkcje różniczkowanie wyraz za wyrazem [8°, 438], przekonamy się łatwo, że
(17) C'(jc) = -5(jc), S'(x) =C(x).
Jak widzieliśmy, wszystkie te własności można łatwo wyprowadzić. Trochę więcej wysiłku wymagać będzie dowód okresowości rozpatrywanych funkcji, do czego teraz przejdziemy.
Stwierdzimy najpierw, że w przedziale (0, 2) istnieje dokładnie jeden pierwiastek funkcji C (jc). Rzeczywiście, wiemy, że C (0) = 1. Natomiast wartość C(2) można zapisać w postaci
C( 2) =
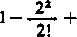
2*
4!
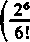
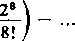
(wydzielając trzy pierwsze wyrazy odpowiedniego szeregu a pozostałe łącząc parami). Ponieważ wyrażenia w każdym nawiasie są dodatnie
2ł" 22"+2 22" L 2-2 \ >{)
(2/i)! (2/i+2)! “ (2«)! \ (2/i+ł) (2//+2) / ’
a suma pierwszych trzech wyrazów jest równa — y , więc C (2)< ~ , tzn. C (2) jest ujemne. Ponieważ funkcja C (jc) jest ciągła, wynika stąd, że funkcja ta rzeczywiście ma pierwiastek w przedziale (0,2).
Z drugiej strony, w tym właśnie przedziale funkcja
5 (jc) = jc
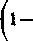
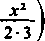
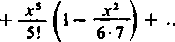
zachowuje oczywiście znak dodatni, a pochodna C%v) — — 5(jc) ujemny, a więc funkcja C(.v) maleje od 0 do 2 i raz tylko przyjmuje wartość 0.
Oznaczmy teraz znaleziony pierwiastek funkcji C (jc) przez -y rr; liczbę n wprowadzamy tu, ja k widać w sposób całkiem formalny i nie należy utożsamiać jej ze stosunkiem obwodu kola do średnicy.
Mamy więc:
C(fr) = °, 5(|w)=l.
Ostatnia równość wynika z (16) po uwzględnieniu tego, że funkcja 5 (jc) jest dodatnia dla 0<x<2.
Przyjmując we wzorach (14) i (15) najpierw x = y = y rr, a następnie x = y — n, otrzymujemy kolejno:
C(jt) = -1, 5(n) = 0: C(2jt) = 1, 5(2n) = 0 .
Jeżeli we wzorach tych, przy dowolnym jc przyjmiemy y = k lub y — 27t, to otrzymujemy (18) C Cv+7c) = - C (jc), 5 (*+*) = -5 (jc)
Wyszukiwarka
Podobne podstrony:
370 XII. Ciągi i szeregi funkcyjne Dla liczby ct [429] znajdziemy taki wskaźnik ą, że
378 XII. Ciągi i szeregi funkcyjne Tutaj J o więc szereg można całkować wyraz za wyrazem, mimo że dl
386 XII. Ciągi i szeregi funkcyjne Jeżeli dla funkcji /(x) otrzymamy rozwinięcie w szereg potęgowy t
400 (5) XII. Ciągi i szeregi funkcyjne 10) Rozpatrzmy rozwinięcie (dla
402 XII. Ciągi i szeregi funkcyjne Szeregi te można też wykorzystać dla rachunków przybliżonych.
420 XII. Ciągi i szeregi funkcyjne szereg ten jest zbieżny dla — 1 <x<. Równość CO £ (2x-x*)m
430 XII. Ciągi i szeregi funkcyjne Korzystąjąc z rozwinięcia (12) dla dostatecznie małych / mamy ^(—
448 XII. Ciągi i szeregi funkcyjne 457. Funkcja wykładnicza. Widzieliśmy [404, (11)], że dla dowolne
452 XII. Ciągi i szeregi funkcyjne Naturalne będzie określenie funkcji cos z i sin z dla dowolnego z
464 XII. Ciągi i szeregi funkcyjne Twierdzenie odwrotne nie jest jednak prawdziwe: różne funkcje mog
11233 Strona�3 S 3óó XII. Ciągi i szeregi funkcyjne W drugim przypadku wysokość garbów, które przesz
364 XII. Ciągi i szeregi funkcyjne 428. Zbieżność jednostajna i niejednostajna. Przypuśćmy, że
366 XII. Ciągi i szeregi funkcyjne W drugim przypadku wysokość garbów, które przeszkadzają w
368 XII. Ciągi i szeregi funkcyjne 429. Warunek jednostajnej zbieżności. Twierdzenie
372 XII. Ciągi i szeregi funkcyjne Twierdzenie 1. Niech funkcje u„{x) (n = 1,2,3,...) będą określone
374 XII. Ciągi i szeregi funkcyjne 432. Uwaga o zbieżności ąuasi-jednostajnej. Jeżeli szereg funkcyj
376 XII. Ciągi i szeregi funkcyjne Odejmując tę równość wyraz po wyrazie od (11) łatwo otrzymujemy(1
380 XII. Ciągi i szeregi funkcyjne w którym suma pierwotnego szeregu nie może mieć pochodnej, gdyż j
więcej podobnych podstron