0452

454

XII. Ciągi i szeregi funkcyjne

Ograniczymy się do wartości głównej logarytmu

z = — In (h>i± ]/l —w²) . i

Dla w = +1 lub —1 pierwiastek staje się równy 0 i otrzymujemy odpowiednio z = -i-rc lub — yjt, co przyjmujemy jako wartość główną arcusa sinusa. Niech teraz będzie w^± 1, musimy dokonać wyboru jednej z dwóch-wartości z. Oczywiście

(wi-l- j/1 — w²) (wi— — tv²) = 1 ,

tak że

— In (*'/'+ j/l — tv²) + — ln (w/ — ]/l — w²) =    ,

i    i

a więc

R ^-i-ln(H'/+ l/l-w²)j +R ^4

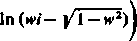
±ir,

podczas gdy części urojone różnią się tylko znakiem. Ponieważ żadna z części rzeczywistych nie wychodzi poza przedział (—n, 7t>, więc tylko jedna z nich będzie zawarta między — y rc i y n; odpowiednią wartość funkcji przyjmujemy jako główną. Wyjątkową sytuację otrzymamy tylko w przypadku, gdy obie części rzeczywiste są równe y n lub — y n, wtedy jako główną przyjmujemy tę wartość, której odpowiada część urojona dodatnia!¹)- Z tym zastrzeżeniem można powiedzieć, że wartość główną funkcji arcusa sinus otrzymamy z warunku

—j n < R (arc sin w) < -i- n .

Łatwo sprawdzić, że pozostałe wartości otrzymamy ze wzorów Arc sin w = arc sin wĄ-lkn ,

Arc sin w = (2k+1) n—arc sin w {k — liczba całkowita).

Na zakończenie zatrzymamy się na rozwinięciu arc sin w według potęg w. W przypadku zmiennej rzeczywistej widzieliśmy już, że odwróceniem szeregu

y =

+(-!)"-

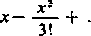
X¹’-¹

(2n— 1)!

określającego sin x jest szereg

Jt = y+4-• 4-+

1- 3

2- 4

2l    (2/i — D!! y^ł"⁺¹ .

5    (2n)!! 2n+l

określający arc sin y [patrz 440, 3)]. Ponieważ w przypadku zmiennej zespolonej współczynniki obliczamy w ten sam sposób, widać, że odwróceniem szeregu

+(-!)"

(2/i-1)!

musi być szereg

H-+ ■

W

3

+

13

2-4

+ ... +

(2/1-1)!!

(2 *)!!

w²"⁺¹ 2n+1

(^l) Na przykład arc sin 2 = y tt+i ln (2+ j/3).