24 luty 07 (56)

Założymy, że wał wirnika jest konstrukcyjnie i technologicznie wyrównoważo-ny. Stan wyrównoważenia wirnika będzie zatem wynikał z położenia środków mas S_? i S₂, odpowiednio dla mas i m₂.

Uwzględniając położenie środków mas S₁ i S₂, otrzymamy cztery warianty stanu wyrównoważenia przedstawione kolejno na rysunkach rysunkach 3.76- 3.79.

y

^xs = o, y_s * 0, B = B₁ + b₂ * o D_xz = 0, Dy_z = 0, Mg — 0

x_s=o, y_s =0, B =0

D_xz — 0, Dy_z ⁼ 0, Mg — 0

Rys. 3J7. Wirnik niewyrównoważony B *0, niewyrównoważenie siłowe

Rys. 3.76. Wirnik wyrównoważony

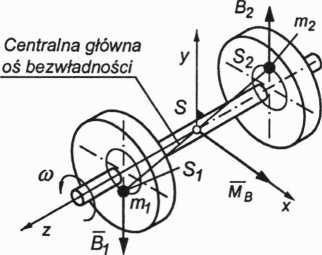
x_s =0, y_s =0, B = S, +B₂=0 D_xz = 0, D_yz * 0, Mg * 0

x_s*0, y_s*0, B = B₁+B₂*0 D_xz * 0, D_yz 0, Mg z 0

Rys. 3.79._Wirnikniewyrównoważony B *Ó, M_b * Ó. Przypadek ogólny

Rys.^.78. Wirnik niewyrównoważony M_B *0, niewyrównoważenie momentowe

206