50 (229)

180 ODPOWIEDZI. WSKAZÓWKI. ROZWIĄZANIA

396. «-2>' + 4 = 0.

Wskazówka. Wykonaj rysunek. Poprowadź prostą równoległą do boku Mt przechodzącą przez punki /’.

397. a) (-1.3). (ó. 2); b) pole: 15.

398. (" = (0.3) lub C = (12. 15).

Rozwiązania. Pole trójkąta ABC: f'~0.5 | Ali \ ■ <1. gdzie djcsl odległością punktu C od powiej AB. Długość odcinka AB jest równa 2*5. Równanie prostej AB: 2\->•—3=0.

Punk! (' należy do pioslej k. więc C-(p. p 3), gdzie /* jesl pewną liczba rzeczywistą.

|7 .. i _nX1l II I .« <11

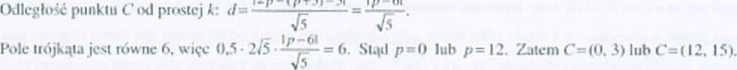
399. <4--/*. ^3). (4+yfJ. -V3).

Rozwiązanie. AT = («_A. y*) - punki styczności okręgu wpisanego w trójkąt ABC7. bokiem AB. •

CS =|2,2). SK =|.u-3.yA+ I). .VA' =0.5-CS =|l. IJ. Zatem ar* -3=1 i v* + I = l.stąd A=(4.0).

Równanie prostej I. prostopadłej do CS i przechodzącej przez, punkt K: r i v-4=0.

S jesl również środkiem okręgu opisanego na tiójkącic ABC. a punkty 4 i B są punktami wspólnymi lego ••kręgu i pioslej k. Równanie okręgu (ĄS, ICM): (i-3 )■ + (y +1)^: = 8.

Współrzędne punktów4 i B znajdujemy, rozwiązując układ równań a +y-4=0 i (r-3)* + (_v+ I )‘ = X:

(t, vJ=(4-^3. fi) lub (a,y)=(4+^3. — ^3).

400. y = — r + 4. y= I lub y = —r + 4. r = 3.

Wskazówka. ABC - rozważany trójkąt. Jeśli punkt C jest wierzchołkiem kąta prostego trójkąta ABC. to punkt /(jest punktem wspólnym prostej o równaniu \ y + I = 0 i okręgu o środku w punkcie C i promieniu długości |.lć’|.

401. (ff).

402. 0 = (6.3>. <7= i-l. 1(0.

403. zt=(l,4). fl=(5. 12). C-|V. 10)

Rozwiązanie. Punkt B nale/y do prostej o równaniu y 2i + 2. więc B=(b. 27* + 2). gdzie h jest pewną liczbą rzeczywistą.

Punkt C należy do prostej o równaniu a = 3y 21. więc C=(3c 21. < ), gdzie r jest pewną liczbą rzeczywistą.

BC - |3r-2l - A. c <2A + 2)J = |4. —2|. w ięc 3<*-2I - A=4 i . -2A-2=-2. Rozwiązaniem otrz.ym.mego układu równań jest para liczb A=5 i c= 10. Zatem tf=tS.I2).C=(9.10).

Środek S odcinka AB jest punktem wspólnym prostych o równaniach y - 2r + 2 i «-3y + 21 -0. Rozwiązaniem układu równań y = 2r+2 i X - 3> + 21 ■ I) jest para liczb (».>) = <3. Xi. więci'=(3. X).

Korzystając ze wzorów na współrzędne śiislka odcinka, znajdujemy współrzędne punktu A: 4 = ( 1.4).

404. 4 = (-7. 51. B (-4,-1). Z)s=(-6, 3).

405. (.v-l)²+(y + ^)²=|.

406. B ■ (-5.4). C = (3. I).

Rozwiązanie. Niecił S i K będą odpowiednio punktem wspólnym środkowych trójkąta ABC i śriHlkieni odcinka BC.

Rozwiązując układ równań 4t + 5.v = 0 i i - 3v = 0. znajdujemy współrzędne punktu S: S = (0. 0). Z równości AS - 2 SK wyznaczamy współrzędne punktu K: A'=(-1, 2.5 >.

Szukane punkty mają współrzędne (/>. -0.8A) i (3<\ cl (Iw należy tloprostych o równaniach odpowiednio y -<).Xi i a - 3y), gdzie b i c są pewny mi liczbami rzeczywistymi. I*unkt A" jest środkiem odcinka AB. więc -I - 0.5(/> + .V) i 2.5 0.5(-0,8A + c). Rozwiązaniem otrzymanego układu równań jest para i />. r>=(-5. 11. Zatem pozostałe wierzchołki trójkąta ABC mają Współrzędne (-5. 4> i (3. li.

407. A = (I, -4). // = (6. 1). C = <-2. 17).

Wskazówka. Znajdź obraz punktu B w symetrii względem prostej o równaniu 31 —>•—7—(1.

409. a) 2x + 3y + I ■ 0; b) />=(—2. I): c)7X.

410. a) y a; b) C=(6.f»). Z>=(-ó.0).

Rozwiązanie. Niech = y/>). Punkt .V jest środkiem odcinka BI). Korzystając ze wzorów na współrzędne środka mlcinka. otrzymujemy