CCF20090303041

86 Argument na rzecz indeterminizmu

Przekrój tego podwójnego stożka wygląda następująco:

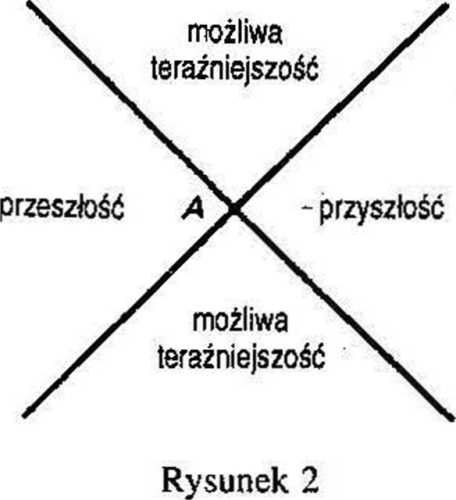
(Rysunek ten ustawiłem w taki sposób, aby czas wskazywał od lewej do prawej strony, jak to się zwykle czyni na diagramach, aczkolwiek na diagramach teorii względności oś upływu czasu przebiega zazwyczaj od dołu ku górze*)

Nie będę omawiał szczegółów tego dobrze znanego diagramu. Chciałbym jednak wskazać na to, że spełnia on całkowicie wymóg asymetrii między przyszłością i przeszłością. W terminach fizyki asymetria ta opiera się na fakcie, że z dowolnego miejsca w „przeszłości” fizyczny łańcuch przyczynowy (na przykład sygnał świetlny) może sięgnąć dowolnego miejsca w przyszłości, ale z żadnego miejsca w przyszłości nie można wpłynąć na jakiekolwiek miejsce w przeszłości¹.

Werdykt szczególnej teorii względności

W konsekwencji jednak przyszłość staje się „otwarta” dla nas w tyra sensie, że nie możemy jej przewidzieć w całej pełni, podczas gdy przeszłość jest zamknięta. Oznacza to właśnie tę asymetrię, którą starałem się udowodnić.

Aby to zrozumieć, przyjmujemy, że znajdujemy się w punkcie A i chcemy dokonać wyczerpującego przewidywania stanu naszego świata, gdy znajdzie się on w czasoprzestrzennym punkcie B.

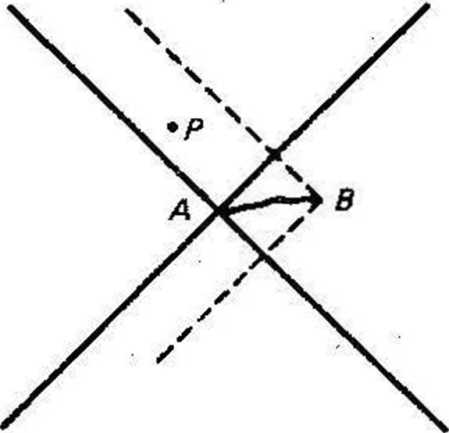
Rysunek 3

Wiadomo powszechnie², że nie potrafimy tego dokonać: jak wskazuje rysunek 3, istnieją takie punkty jak P, należące do przeszłości B, lecz nie do przeszłości A, co znaczy, że w punkcie P mogą zachodzić oddziaływania wpływające na punkt B, lecz nie leży w naszych możliwościach, gdy znajdujemy się w punkcie A, uzyskać jakąkolwiek informację o warunkach w punkcie P, ponieważ żadne oddziaływania z punktu P nie są nam w punkcie A dostępne: P jest poza

Pod tym względem ogólna teoria względności różni się od szczególnej teorii, co wykazał Godeł (por. przypis poprzedni). Nie ma wątpliwości, że rozwiązania wspomniane przez Gódla nie zgadzają się z ideami leżącymi u podłoża teorii ogólnej, jak zasugerował Einstein (Albert Einstein, Philosopher-Scientist, op. cit„ s. 688) i że należy je wykluczyć. Jednakże rozwiązanie ad hoc byłoby niewystarczające. O ile wykluczenie nie wynika z modyfikacji samych równań, można polegać na następującej „zasadzie nieprzerwanych połączeń linii kosmologicznych {world-lines}'\ Jest to zasada, która według mnie zawiera się w samej idei czasu lokalnego, jak i w zasadzie, że szczególna względność musi obowiązywać lokalnie w teorii ogólnej. W terminach operacyjnych tę moją zasadę można sformułować następująco: Dowolny „obserwator” (lokalny system materialny) może w dowolnym momencie rozpocząć rejestr ciągu przyczynowego, wprowadzać do niego nowe dane i czynić przygotowania mające na celu zachowanie tego rejestru przez dowolnie długi czas. (Przez wyraz „może” rozumiem rzecz następującą: teoretyczna możliwość dowolnej linii kosmologicznej, uznawanej za nie-sprzeczną z prawami natury, nie musi implikować niemożliwości czynności opisanych w powyższej zasadzie.) Jeżeli przyjmiemy tę zasadę, wówczas istnienie „obserwatora” (systemu materialnego), którego linie kosmologiczne są zamknięte w czasie, prowadzi

do sprzeczności. Można bowiem łatwo wykazać, że istnienie zamkniętej linii kosmologicznej (która z uwagi na spójność musiałaby być nieskończenie i absolutnie repety-tywna) implikowałaby okresową destrukcję każdego rejestru (ciągu przyczynowego), ponieważ inaczej ciąg (lub ślad przyczynowy) nie byłby w pełni repetytywny, lecz stale wzbogacał się przy każdym powtórzeniu podróży przebiegającej po linii zamkniętej. Przyjęcie mojej zasady spowodowałoby, że „sposób rozkładu materii i jej ruchu w świecie” (op. cit., s. 562) zależałby od jego struktury czasowej (którą moja zasada pomaga opisać), nie zaś odwrotnie. Ten sam wynik można otrzymać - w sposób, który nie ma tak wyraźnego charakteru ad hoc - przyjmując „zasadę indeterminizmu"; ona również wykluczałaby automatycznie wszystkie kosmologiczne rozwiązania dopuszczające istnienie zamkniętych linii kosmologicznych.

¹⁷ Por. Hermann Weyl, Philosophy of Mathematks and Natural Science, Princeton 1949, s. 210, 102.