8903649923

Notatki do lekcji, klasa matematyczna - Mariusz Kawecki, U LO w Chełmie

b) Liczba jest mniejsza od 0 i jej kwadrat nie jest mniejszy od 0, stąd: jeżeli liczba jest mniejsza od 0, to jej kwadrat jest większy od 0.

c) Liczba 2 jest większa od 0, stąd: nieprawda, że liczba 2 jest mniejsza od 0.

d) Nieprawda, że 1 równa się 0 lub 1 równa się 2, stąd: 1 jest różny od 0 i 1 jest różny od

2.

e) Nieprawda, że x jest większe bądź równe -1 i x jest mniejsze bądź równe 1 oznacza, że x jest mniejsze od -1 lub x jest większe od 1.

Zwykle twierdzenia matematyczne zapisuje się w postaci implikacji, gdzie z przesłanek wynika pewien wniosek p=>q, ,.jeżeli suma cyfr liczby dzieli się przez 3 to liczba dzieli się przez 3”. Takie twierdzenie nazwiemy prostym. Twierdzenie odwrotne, to twierdzenie <7=> p, jeżeli liczba dzieli się przez 3 to suma jej cyfr dzieli się przez 3”. Twierdzeniem przeciwnym nazywamy twierdzenie —i p=>—\q, Jeżeli suma cyfr liczby nie dzieli się przez 3, to liczba nie dzieli się przez 3”. Twierdzeniem przeciwstawnym (kontrapozycją) nazwiemy twierdzenie —\q=>—\ p, Jeżeli liczba nie dzieli się przez 3, to suma jej cyfr nie dzieli się przez 3”. Łatwo jest sprawdzić, że pomiędzy twierdzeniami prostym a przeciwstawnym oraz odwrotnym a przeciwnym zachodzi równoważność. Innymi słowy tautologiami są schematy:

(p => q) <=> (-, q => -i p)

(<7 => p) <=> (-1 p => i q)

W praktyce oznacza to, że zamiast uzasadniać twierdzenie proste można uzasadnić twierdzenie przeciwstawne, co może okazać się łatwiejsze. Powyższe wywody prowadzą do tak zwanego kwadratu logicznego (rys. 3), w którym opisane powyżej przypadki umieszcza się schematycznie w rogach kwadratu.

P=><7 <7=>P

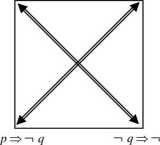
Rysunek 3

Implikacje stojące na przekątnych tego kwadratu mają tę samą wartość logiczną, obie są prawdziwe lub obie są fałszywe. Jeżeli dowiedziemy, że implikacje stojące przy dowolnym boku obie są prawdziwe, oznaczać to będzie, że wszystkie implikacje w kwadracie są prawdziwe. Jeżeli dwie implikacje stojące przy tym samym boku okażą się fałszywe, to wszystkie implikacje w kwadracie będą fałszywe.