9742848388

Notatki do lekcji, klasa matematyczna - Mariusz Kawecki, U LO w Chełmie

le setek lat zanim stwierdzono, że nie są one wykonalne. Przykładem tego typu zadań mogą być trzy klasyczne problemy rozpatrywane jeszcze przez starożytnych.

Podwojenie sześcianu (tzw. problem delijski). Podczas trwania zarazy w Atenach, mieszkańcy miasta wysłali przedstawicieli do wyroczni Apollona na wyspie Delos, z pytaniem, co zrobić, aby powstrzymać zarazę. Wyrocznia orzekła, że zaraza wygaśnie, jeżeli ateńczycy podwoją ołtarz Apollona, który miał kształt sześcianu. Jak przeprowadzić konstrukcję, aby życzeniu Apollona stało się zadość? Tyle legenda. Przez dwa tysiąclecia matematycy i nie tylko głowili się nad tym problemem. Niech sześcian do podwojenia ma bok a. Bok podwojonego sześcianu oznaczmy przez x, problem prowadzi do następującego równania:

x³ = 2 a³

x =    2

Okazuje się, że nie jest możliwe skonstruowanie odcinka o długości    2 posługując się tylko

cyrklem i linią.

Kwadratura koła. Innym ważnym problemem geometrycznym starożytnych było skonstruowanie przy pomocy cyrkla i linijki kwadratu, którego pole równe jest polu danego koła. Przekładając ten problem na język algebry otrzymamy:

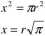
Dopiero w 1882 roku niemiecki matematyk Carl Lindemann pokazał, że konstrukcja odcinka o długości r-Jn nie jest możliwa (dokładniej pokazał, że n jest tzw. liczbą przestępną, z którego to faktu wynika niemożność takiej konstrukcji. Sama nazwa kwadratura koła weszła do języka potocznego jako synonim czegoś niewykonalnego.

Trysekcja kąta. Trzeci wielki problem starożytnych związany był z konstrukcją podziału dowolnego kąta na trzy kąty przystające. Kąty można podzielić na dwie grupy, takie, które dadzą się podzielić przy pomocy cyrkla i linijki na trzy kąty przystające (np. kąt prosty) oraz takie, których w ten sposób podzielić niemożna. Niemożność takiej konstrukcji po raz pierwszy uzasadnił książę matematyków Carl Gauss (w wieku 9 lat). Ścisły dowód tego faktu przeprowadził w 1837 roku matematyk francuski Pierre Wantzel.

Określenie 16. Symetralną odcinka nazywamy prostą prostopadłą do odcinka i dzielącą go na dwa odcinki przystające.

Twierdzenie 6. Symetralna jest zbiorem punktów jednakowo odległych od końców odcinka.

Dowód. Odcinek i jego środek wyznaczają kąt półpełny, symetralna dzieli go na dwa kąty przystające (kąty proste), więc symetralna może być traktowana jak dwusieczna kąta półpeł-nego, zatem jest zbiorem punktów jednakowo odległych od ramion tego kąta a tym bardziej od końców odcinka. □

17