9742848395

Notatki do lekcji, klasa matematyczna - Mariusz Kawecki, U LO w Chełmie

PODSTAWOWE OKREŚLENIA I AKSJOMATY

Z obserwacji potocznej wiemy, że wyróżniając na płaszczyźnie jakiś punkt możemy przez ten punkt poprowadzić linie proste. Potraktujmy tę obserwację jako pewnik.

Aksjomat I. Przez każdy punkt płaszczyzny przechodzi nieskończenie wiele prostych. Każda prosta zawiera nieskończenie wiele punktów.

Określenie 1. Zbiór wszystkich prostych przechodzących przez punkt A nazywamy pękiem prostych o wierzchołku A i oznaczamy (A).

Pewnik gwarantuje, że prostych w pęku jest nieskończenie wiele. Zauważmy, że pokrywają one całą płaszczyznę. Ostatnia uwaga oznacza, że oprócz wierzchołka A każdy inny punkt płaszczyzny należy do pęku (A) gdyż należy do jakiejś prostej przechodzącej przez ten wierzchołek. Powstaje pytanie, na jakiej podstawie twierdzimy, że proste z pęku pokrywają całą płaszczyznę. Innymi słowy skąd wiemy, że dla dowolnego punktu płaszczyzny znajdziemy prostą należącą do pęku, która zawiera ten dowolny punkt. Gwarantuje to kolejny pewnik.

Aksjomat II. Przez dwa punkty płaszczyzny przechodzi dokładnie jedna prosta.

Przyjmując prawdziwość ostatniego zdania widzimy, że dowolny punkt płaszczyzny np. fi i wierzchołek pęku A wyznaczą prostą. Prosta ta jako przechodząca przez A należy do pęku o wierzchołku A, to z kolei oznacza, że punkt B również należy do pęku, dlatego pęk pokrywa całą płaszczyznę (punkt B wybraliśmy przecież dowolnie).

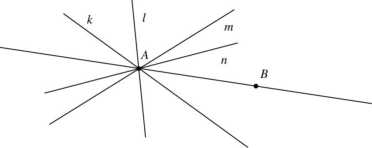
Jedna z prostych pęku A przechodzi również przez punkt B, który wybrano dowolnie. Można powiedzieć, że przez dowolny punkt płaszczyzny przechodzi jakaś prosta należąca do pęku (Aj albo pęk (A) pokrywa płaszczyznę.

Innymi słowy, aby wyznaczyć prostą wystarczą dwa punkty. Zauważmy, że nie ma znaczenia czy prosta ma leżeć na płaszczyźnie czy też w przestrzeni (każda prosta w przestrzeni też znajduje się na jakiejś płaszczyźnie), oba pewniki będą równie prawdziwe, gdy występujące w nich słowo „płaszczyzna” zamienimy na słowo „przestrzeń”. Prostą przechodzącą przez punkty A oraz B będziemy oznaczali pr. AB. Zauważmy, że z aksjomatu II można wywnioskować bardzo ważną cechę prostych.

Twierdzenie 1. Jeżeli dwie proste k i / mają dwa punkty wspólne to się pokrywają (stanowią tę samą prostą).

Dowód. Rzeczywiście, jeżeli A i fi są owymi wspólnymi punktami oznacza to, że prosta k te dwa punkty zawiera. Ponieważ przez dwa różne punkty można poprowadzić dokładnie jedną