9742848381

Notatki do lekcji, klasa matematyczna - Mariusz Kawecki, IILO w Chełmie

Ten zapis symboliczny czytamy w następujący sposób: „zbiór nazywamy wypukłym, jeżeli dla każdych punktów A oraz B należących do figury F (symbol e), część wspólna (iloczyn zbiorów, symbol n) odcinka AB oraz figury F równa się odcinkowi AB (czyli wszystkie punkty odcinka AB są punktami figury F).

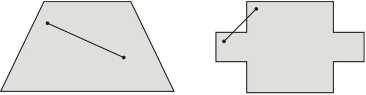
Na rysunku z lewej strony widzimy zbiór wypukły, po stronie prawej zbiór, który wypukły nie jest. Twierdzenie 2. Prosta, półprosta i odcinek są figurami wypukłymi.

Dowód. Wynika wprost z określenia figury wypukłej. Jeżeli weźmiemy jakiekolwiek punkty A i B z prostej, (półprostej lub odcinka), to odcinek AB jest zawarty w prostej (półprostej lub odcinku). □

Prosta, z której usunięto dowolny punkt nie jest wypukła. Podobnie łamana, która nie leży na jednej prostej też nie jest wypukła. Niektóre wielokąty są wypukłe, inne nie. Figury (zbiory) wypukłe mają ważną własność, którą opiszemy twierdzeniem.

Twierdzenie 3. Część wspólna figur (zbiorów) wypukłych jest figurą wypukłą.

Dowód. Jeżeli dwa dowolne punkty A i B należą do części wspólnej figur wypukłych F nG to należą do figury F i należą do figury G. Ponieważ każda z figur jest wypukła, więc zawiera cały odcinek AB, w takim razie odcinek AB zawarty jest w części wspólnej F n G, co dowodzi, że część wspólna jest wypukła. □

Ćwiczenia

1.    Które punkty można usunąć z odcinka, aby pozostał nadal zbiorem wypukłym?

Można usunąć tylko końce odcinka. Jeżeli usuniemy jakikolwiek punkt poza końcami to wybierając punkt „na lewo” od usuniętego i „na prawo” od usuniętego wyznaczymy odcinek, którego nie wszystkie punkty należą do odcinka wyjściowego.

2.    Przy jakich dodatkowych warunkach suma zbiorów wypukłych jest zbiorem wypukłym?

Aby dowolny odcinek o końcach w zbiorach A lub B cały należał do sumy potrzeba i wystarczy, żeby A u B = A lub A u B = B. To oznacza, że B c A lub Aa B. Zatem aby suma zbiorów wypukłych była wypukła, jeden zbiór musi zawierać się w drugim.

3.    Określmy funkcję d(A,B) odwzorowująca pary punktów w zbiór liczb rzeczywistych następujący sposób: d(A,B) = 0, jeżeli A pokrywa się z B, d(A,B) = 1, jeżeli A jest różne od B. Czy tak określona funkcja jest odległością?

10