9742848397

Notatki do lekcji, klasa matematyczna - Mariusz Kawecki, IILO w Chełmie

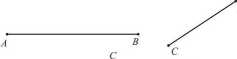
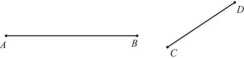
„Pomiędzy” znaczy, że następuje za A i poprzedza fi lub odwrotnie. Zauważmy, że odcinek zawiera nieskończoną ilość punktów i spełnia aksjomat ciągłości Dedekinda. Ponadto z określenia wynika, że odcinek leży na jakiejś prostej. Odcinki można dodawać i odejmować. Odcinki można dodawać i odejmować. Aby dodać dwa odcinki (rysunek pierwszy) odkładamy, na półprostej pierwszy z nich tak, aby jego początek pokrył się z wierzchołkiem pół-prostej, następnie odkładamy na półprostej drugi odcinek tak, aby jego początek pokrywał się z tym końcem odcinka pierwszego, który nie leży w wierzchołku a drugi koniec leżał na półprostej na zewnątrz końców odcinka pierwszego. Przez sumę odłożonych odcinków rozumiemy odcinek, wyznaczony przez wierzchołek półprostej i ten punkt, który leży na zewnątrz końców odcinka pierwszego. Aby dwa odcinki odjąć (rysunek drugi) odkładamy na półprostej dwa odcinki tak, aby początki odcinków pokrywały się z wierzchołkiem półprostej. Przez różnicę dwóch odcinków rozumiemy odcinek wyznaczony przez końce odłożonych odcinków, które nie leżą w wierzchołku półprostej.

Zauważmy, że sumą i różnicą odcinków zerowych jest oczywiście odcinek zerowy. Opisany sposób postępowania zapewnia uzyskanie różnicy bez względu na to czy „mniejszy” odciek odejmowany jest od większego, czy też na odwrót.

A    B    D

A    D    B

Sumą odcinków, AB i CD jest odcinek AD. Różnicą odcinków, AB i CD jest odcinek DB. Zauważmy, że jeżeli od odcinka „mniejszego" odejmiemy odcinek „większy” to nie otrzymamy odcinka „ujemnego" a wynik będzie przystawał do wyniku odejmowania odcinka mniejszego od większego.

Określenie 4 (odległość). Każdej parze punktów A i B na płaszczyźnie można przyporządkować liczbę nieujemną lAfil zwaną odległością w taki sposób, że spełnione są następujące warunki:

1.    Jeżeli punkty A i fi się pokrywają to odległość między nimi wynosi 0, |Afi| = 0 .

2.    Odległość od A do fi jest taka sama jak od fi do A, | Afi| = |fiA|.

3.    Jeżeli dane są trzy różne punkty A, fi, C to zachodzi nierówność |Afi| +|fiC| > |AC|.

Ostatni warunek nazywa się nierównością trójkąta i jest spełniony dla każdej pary punktów, można, więc napisać |AC| + |fiC| >|Afi| lub |Afi| + |AC| >|fiC|. Odległość (inaczej zwana metryką) jest, zatem funkcją odwzorowującą pary punktów na zbiór licz rzeczywistych nieujem-nych. Często zamiast mówić odległość od A do fi mówimy długość odcinka AB (wszak dwa punkty A i 6 wyznaczają odcinek). Zauważmy, że zdefiniowana w ten sposób odległość jest znacznie ogólniejsza od potocznie rozumianej długości gdyż niczego oprócz spełnienia trzech powyższych punktów na funkcję odległości nie narzucamy. Odległością może być, zatem

7