8903649930

Notatki do lekcji, klasa matematyczna - Mariusz Kawecki, IILO w Chełmie

Jest więc:

28-1 + 30-4 + 31-7 = 365

Zatem liczby, których szukamy to x = l, y = 4, z = 7. Zaprezentowane rozumowanie, chociaż zupełnie nieoczekiwane, jest jak najbardziej logiczne i przekonywujące. Jest też inne rozwiązanie równania (1) jc = 2, y = 1, z = 9. Ponieważ w treści zadania chodziło o wskazanie czy taka trójka istnieje, nasza „kalendarzowa metoda” w zupełności jest wystarczająca.

Przykład 2

W ziemię wbito dwa kołki, każdy o wysokości 1 m. Pomiędzy kołkami wisi sznurek, zaczepiony przy wierzchołkach, który ma również 1 m. długości. Sznurek wisi swobodnie w taki sposób, że najniższy jego punkt znajduje się 0,5 m. nad ziemią. Jaka jest odległość pomiędzy kołkami?

Rysunek 1

W tym przykładzie metoda rozwiązania jest jeszcze prostsza. Skoro najniższy punkt sznurka wisi 0,5 m. nad ziemią, to zarazem znajduje się w połowie wysokości metrowego kołka (rys.l). Ponieważ sznurek ma 1 m. długości więc jest złożony na pół czyli kołki się stykają.

Przykład 3

Dwa promy płyną z przeciwnych brzegów rzeki ze stałymi prędkościami. Pierwszy raz spotykają się 90 m. od jednego z brzegów. Każdy dopływa do brzegu przeciwległego, natychmiast zawraca i płynie z powrotem. Drugi raz spotykają się 50 m. od drugiego brzegu. Jaka jest szerokość rzeki?

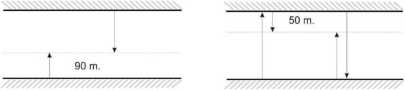
Rysunek 2

Zauważmy, że przy pierwszym spotkaniu promów suma dróg, które przebyły równa jest szerokości rzeki (rys. 2). Przy drugim spotkaniu suma dróg równa jest trzem szerokościom rzeki. Ponieważ prędkość promów nie ulega zmianie czas pomiędzy pierwszym a drugim spotkaniem będzie dwukrotnie dłuższy niż czas do pierwszego spotkania (do pokonania jest dwukrotnie większy dystans). W takim razie pierwszy prom pokona całkowitą odległość 90 + 2-90 = 270m. i ta odległość będzie o 50 m. większa od szerokości rzeki (ponieważ prom zawrócił i płynął 50 m. w stronę przeciwną). Wobec tego szerokość rzeki wynosi 220 m.