9742848398

Notatki do lekcji, klasa matematyczna - Mariusz Kawecki, IILO w Chełmie

intuicyjnie pojmowaną długość, która oznacza ile razy jakiś wybrany odcinek jednostkowy zmieścił się w odcinku mierzonym jak również odległością może być ta długość dzielona przez 2. Obie funkcje spełniają warunki (1)...(3). Świadomi tego, że funkcja odległości może być bardzo różnorodna pozostaniemy przy jej elementarnej interpretacji tzn. przez odległość między punktami rozumieć będziemy liczbę, która oznacza ile razy odcinek jednostkowy zmieścił się w odcinku wyznaczonym przez te punkty. Nierówność w warunku trzecim przechodzi w równość, jeżeli punkt C leży na odcinku AB. W praktyce to oznacza, że każde „zejście” z linii prostej powoduje, iż odległość nam wzrasta. Innymi słowy odległość najkrótsza to odległość wzdłuż linii prostej. Niebawem będziemy dysponowali narzędziami umożliwiającymi dowiedzenie tego spostrzeżenia, do którego tak jesteśmy przyzwyczajeni, że wydaje się oczywiste. Aby móc odmierzać odcinki tzn. porównywać ich długości, konieczne jest przyjęcie następującego aksjomatu.

Aksjomat V. Na każdej półprostej istnieje dokładnie jeden punkt, którego odległość od początku tej półprostej równa jest danej liczbie nieujemnej.

Z Aksjomatu V wynikają ważne wnioski. Po pierwsze, na prostej po obu stronach dowolnego punktu A można znaleźć dwa inne punkty B\ oraz 62 takie, że: |Afi, | = \AB₂\ = n, gdzie n jest dowolną liczbą nieujemną. Po drugie, pomiędzy zbiorem punktów na prostej a zbiorem liczb rzeczywistych można ustalić wzajemnie jednoznaczne przyporządkowanie, które nazywamy osią liczbową. Oś liczbowa pozostaje domeną algebry i na lekcjach algebry zostanie szczegółowo omówiona.

Określenie 5. Jeżeli wyróżnimy na płaszczyźnie jakiś punkt S, to zbiór punktów jednakowo oddalonych (o odległość r) od wyróżnionego punktu nazywamy okręgiem o środku S i promieniu r, co zapisujemy: 0(S, r). Jeżeli rozpatrywać będziemy zbiór punktów, których odległość od punktu S będzie mniejsza lub równa r, to taki zbiór nazywamy kołem o środku S i promieniu r, co zapisujemy: K(S,r). Jeżeli zbiór punktów będzie taki, że odległość każdego punktu ze zbioru od punktu S będzie mniejsza od r, to nazwiemy go wnętrzem koła o środku S i promieniu r, co zapisujemy W(S,r).

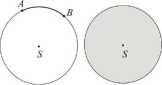
Okrąg, luk AB, koło i wnętrze koła o środku S i promieniu r.

Zauważmy, że jeden punkt nie podzieli okręgu na dwa zbiory (w przeciwieństwie do prostej, którą dzielił). Aby podzielić okrąg potrzebujemy dwóch punktów.

Określenie 6. Wyróżnijmy na okręgu dwa punkty A i B. Zbiór punktów położonych na okręgu pomiędzy punktami A i fi (w porządku zgodnym z ruchem wskazówek zegara) wraz z tymi punktami nazywamy łukiem o końcach A, fi i oznaczamy AB .

Określenie łuku nie będzie jednoznaczne, jeżeli nie podamy porządku. „Pomiędzy” punktami A i fi może przecież oznaczać jeden z dwóch zbiorów, wyznaczanych na okręgu przez dwa punkty. W trakcie dalszej nauki poznamy pojęcie orientacji płaszczyzny, które pozwoli nam