9742848390

Notatki do lekcji, klasa matematyczna - Mariusz Kawecki, IILO w Chełmie

Określenie 18. Kąty nazywamy wierzchołkowymi, jeżeli są wypukłe, mają wspólny wierzchołek oraz ich ramiona uzupełniają się do prostej.

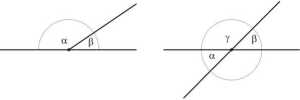
Kąty przyległe i kąty wierzchołkowe.

Twierdzenie 7. Kąty wierzchołkowe są jednakowe (przystające).

Dowód. Kąty a i y tworzą parę kątów przyległych. Drugą parę kątów przyległych tworzą kąty y i fi. Mamy, więc: a + y=y + J3 a = fi

Określenie 19. Weźmy na płaszczyźnie trzy proste k, l, m. Niech jedna z nich k nie będzie równoległa do pozostałych. Ta wyróżniona prosta k tworzy z pozostałymi dwiema prostymi /, m sześć grup par kątów.

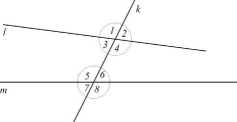
a)    kąty odpowiadające są to pary kątów: 1 i 5, 3 i 7, 2 i 6, 4 i 8,

b)    kąty naprzemianległe wewnętrzne są to pary kątów: 3 i 6, 4 i 5,

c)    kąty naprzemianległe zewnętrzne są to pary kątów: 1 i 8, 2 i 7,

d)    kąty jednostronne wewnętrzne są to pary kątów: 3 i 5, 4 i 6,

e)    kąty jednostronne zewnętrzne są to pary kątów: 1 i 7, 2 i 8.

f)    kąty wierzchołkowe (w myśl wcześniejszego określenia): 1 i 4, 2 i 3, 5 i 8, 6 i 7.

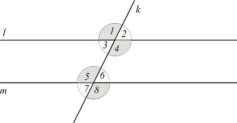
Twierdzenie 8. Jeżeli proste / i m są równoległe to pary kątów odpowiadających są przystające, pary kątów naprzemianległych wewnętrznych są przystające, pary kątów naprzemianle-głych zewnętrznych są przystające, suma kątów jednostronnych równa jest kątowi półpełne-

19