9742848383

Notatki do lekcji, klasa matematyczna - Mariusz Kawecki, IILO w Chełmie

PROSTA, PŁASZCZYZNA, KĄTY. PIERWSZE KONSTRUKCJE

Określenie 11. Podobnie jak dowolny punkt na prostej, tak też dowolna prosta na płaszczyźnie dzieli tę płaszczyznę na dwa obszary nieograniczone. Każdy z nich nazywamy stroną prostej. Jeżeli do strony dodamy prostą otrzymamy półpłaszczyznę.

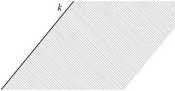
Prosta k podzieliła płaszczyznę na dwa obszary nieograniczone (strony prostej). Jeżeli do strony prostej dodamy prostą k otrzymamy półpłaszczyznę.

Określenie 12. Weźmy dwie proste k i / na płaszczyźnie, które nie mają punktów wspólnych (mówi się są równoległe). Te dwie proste wyznaczają cztery półpłaszczyzny. Interesują nas dwie z nich, półpłaszczyzna wyznaczona przez prostą k i zawierająca prostą /, oraz półpłasz-czyzna wyznaczona przez prostą / i zawierająca prostą k. Część wspólna tych półpłaszczyzna nazywana jest pasem.

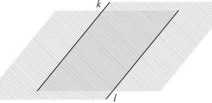
Jeżeli prosta k jest równoległa do prostej l, to iloczyn półpłaszczyzny wyznaczonej przez k i zawierającej l oraz półpłaszczyzny wyznaczonej przez l i zawierającej k jest pasem o krawędziach k i l.

Powstaje pytania skąd wiemy, że takie proste bez punktów wspólnych (albo proste równoległe) w ogóle istnieją na płaszczyźnie? Zapewnia o tym kolejny aksjomat, który przyjmiemy zwany pewnikiem Euklidesa.

Aksjomat VI (Aksjomat równoległości Euklidesa). Dla każdej prostej k na płaszczyźnie i każdego punktu A nieleżącego na tej prostej, istnieje dokładnie jedna prosta l przechodząca przez punkt A i równoległa do prostej k (niemająca z prostą k punktów wspólnych).

W Elementach Euklidesa aksjomat równoległości występujący tam jako piąty był sformułowany w nieco innej formie. Niebawem powrócimy do oryginalnego sformułowania aksjomatu równoległości oraz podamy inne jego równoważne postacie. Przypomnijmy, że wszystkie twierdzenia i określenia, które nie wymagają aksjomatu równoległości tworzą tzw. geometrię absolutną. Twierdzenia i określenia, do których aksjomat równoległości jest niezbędny tworzą geometrię euklidesową. Jeżeli zamiast aksjomatu równoległości użyjemy jego zaprzeczenia, to tak zbudowana geometria nazywa się geometrią nieeuklidesową. Oczywiście pas jako iloczyn figur wypukłych (półpłaszczyzn), jest figurą wypukłą.

Oprócz punktów prostej k oraz prostej /, która jest równoległa do k i przechodzi przez A istnieje na płaszczyźnie dowolnie dużo innych punktów. Weźmy punkt A\ różny od punktów prostej k i l. Zgodne z aksjomatem VI można przez ten punkt poprowadzić prostą l\, która jest

12