9742848399

Notatki do lekcji, klasa matematyczna - Mariusz Kawecki, IILO w Chełmie

wyeliminować mało matematyczne określenie „zgodnie z ruchem wskazówek zegara”. Zarówno luk jaki i okrąg spełniają aksjomat ciągłości Dedekinda.

Określenie 7. Zbiór nazwiemy ograniczonym, jeżeli istnieje koło, które go zawiera.

Innymi słowy, jeżeli potrafimy narysować jakiekolwiek koło tak, żeby wszystkie punkty rozpatrywanego zbioru znalazły się w tym kole, to zbiór taki nazwiemy ograniczonym. Odcinek i zbiory złożone ze skończonej liczby punktów są ograniczone, (aby to uzasadnić należy wskazać środek i promień takiego koła), półprosta i prosta nie są ograniczone.

Określenie 8. Jeżeli odcinki na płaszczyźnie połączymy w taki sposób, że koniec jednego odcinka łączy się z początkiem drugiego odcinka, to taki zbiór odcinków nazywamy łamaną. Łamana może być taka, że żadne kolejne dwa odcinki nie będą leżały na jednej prostej oraz żadne dwa odcinki nie będą się przecinały. Łamaną o takich własnościach nazywamy łamaną zwyczajną. Jeżeli początek pierwszego odcinka łączy się z końcem ostatniego odcinak to łamaną nazywamy zamkniętą (łamaną zwyczajną zamkniętą, jeżeli łamana jest i zwyczajna i zamknięta). Przez długość łamanej będziemy rozumieli sumę długości odcinków, z których łamana się składa.

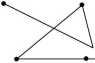
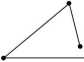
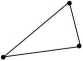
Łamana, łamana zwyczajna, łamana zwyczajna zamknięta.

Określenie 9. Łamana zwyczajna zamknięta dzieli płaszczyznę na dwa obszary. Jeden z nich jest ograniczony. Obszar ten wraz z łamaną nazywamy wielokątem. Długość łamanej jest wtedy obwodem wielokąta. Każdy z odcinków wchodzących w skład łamanej nazywamy bokiem wielokąta. Końce odcinków, które są zarazem początkami innych odcinków nazywamy wierzchołkami wielokąta. Wielokąt o trzech wierzchołkach nazywamy trójkątem, o czterech wierzchołkach czworokątem, o pięciu wierzchołkach pięciokątem itd.

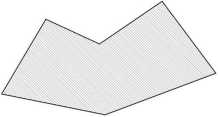
Jeden z obszarów, na który łamana zamknięta dzieli płaszczyznę jest ograniczony, drugi nieograniczony. Obszar ograniczony wraz z łamaną nazywamy wielokątem. Rysunek powyżej przedstawia sześciokąt.

Określenie 10. Figurę geometryczną (dowolny zbiór punktów) nazywamy wypukłą, jeżeli każdy odcinek, którego końce należą do figury, również należy do figury. W symbolice matematycznej figura Fjest wypukła, jeżeli V A,Be F => AB n F = AB.