9742848392

Notatki do lekcji, klasa matematyczna - Mariusz Kawecki, IILO w Chełmie

Powyższe twierdzenie można w sposób zwarty zapisać przy pomocy symboliki logicznej następująco:

< 2 =< 6 <3=<6 «2=«7

<i 4+ < 6 = n

gdzie równości po prawej stronie reprezentują odpowiednie grupy kątów.

Dowód. Przeprowadzimy dla kątów występujących w zapisie symbolicznym. Zauważmy najpierw, że z aksjomatu VI (Euklidesa) wynika, że istnieje dokładnie jedna prosta / równoległa do prostej m i przechodząca przez punkt, który jest wierzchołkiem kąta 2. Dlatego opierając się na pojęciu przystawania możemy stwierdzić, że kąty 2 i 6 są przystające. Ponieważ kąty 2 i 3 są wierzchołkowe, wnioskujemy, że 3 i 6 również przystają. Ponieważ 6 i 7 są wierzchołkowe, przystają także kąty 2 i 7. Aby dowieść ostatniej części twierdzenia zauważmy, że skoro kąty 2 i 6 oraz 4 i 8 przystają prawdziwa jest równość:

< 2+ < 4+ < 6+ < 8 = 2n

< 6+ < 4+ < 6+ < 4 = 2jc 2- < 4 + 2- < 6 = 2n 2-<4 + 2-<6 = 2-/rl:2

< 4+ < 6 = n □

Wspominaliśmy wcześniej, że aksjomat VI (Euklidesa) był przez autora Elementów sformułowany nieco inaczej i oznaczony został jako V. To oryginalne sformułowanie Euklidesa podamy teraz jako twierdzenie, które można wyprowadzić z naszego aksjomatu VI. Możliwa też jest drogo odwrotna, z owego twierdzenia da się wywnioskować aksjomat VI, oznacza to, że podany przez nas aksjomat VI oraz twierdzenie, o którym mowa są równoważne.

Twierdzenie 9. Jeżeli przecinając dwie proste / i m prostą k otrzymamy sumę kątów jednostronnych wewnętrznych mniejszą od 7t to proste l i m przecinają się po tej stronie prostej k, po której leżą sumowane kąty.

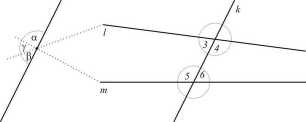
Dowód. Przeprowadzimy metodą nie wprost. Przyjmijmy tezę przeciwną tzn. niech proste / i m nie przecinają się, co oznacza, że są równoległe. Zachodzi wobec tego twierdzenie 8, czyli suma kątów jednostronnych wewnętrznych równa jest n, co przeczy naszemu założeniu. Ustaliliśmy, zatem, że proste muszą się przecinać. Jeszcze raz skorzystajmy z metody nie