0166

168

X. Zastosowania rachunku całkowego

j r

Oczywiście sumy a i .Tsą sumami Darboux dla całki J [g (OffdO; jeśli najwię-

m

ksza z różnic Ad_t dąży do zera, to granice obu sum są równe tej odce (¹), a więc

fi    fi

(9)    |P| = i-/r?d0 = i/[_s (0)Yd6.

a    a

339. Przykłady. 1) Wyznaczyć pole \P\ figury ograniczonej linią łańcuchową v = cosh —, osia x

a

i dwiema rzędnymi, odpowiadającymi odciętym 0 i x (rys. 9).

Mamy tu

X

|/*| =■ f a cosh — dx = a² sinh — = as ,

Ja    a

o

gdzie s oznacza długość luku AM linii łańcuchowej [331, 1)]. W ten sposób szukane pole AOPMokazało się równe polu prostokąta o bokach PS i SM (bowiem SM = AM).

JE* V*

2) Dana jest elipsa -p- + p- = 1 i punkt M (x, y) na niej (rys. 21). Wyznaczyć pole trapezu krzywoliniowego BOKM i wycinka OMB.

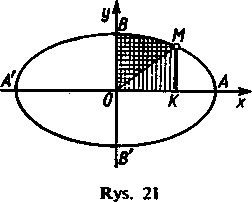
Z równania elipsy mamy y — — ]/a²~x², a więc ze wzoru (7) otrzymujemy dla pola |P_t| figury

a

BOKM wzór

X

\Pi\ — — f y*a²—x²dx —    arcsin — + x ]/a²—x¹ =    arcsin — 4- —■.

a J    2    a 2a    2    a 2

o

Ponieważ ostatni składnik jest równy polu trójkąta OKM, więc odejmując go otrzymamy dla pola \Pj\ wycinka OMB wzór

\Pi\ = — arc sin —.

2    a.

Dla x — a otrzymujemy pole ćwiartki elipsy itab/A, a więc pole całej elipsy jest równe |P| = itab Dla koła mamy a = b = ri wtedy dostajemy znany wzór |P| = w¹.

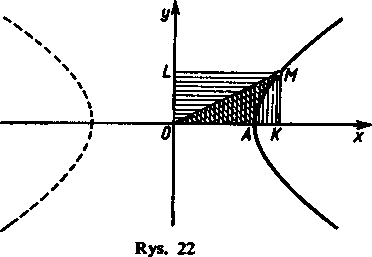
x*    V*

3) Dana jest hiperbola -r- -ry = 1 i punkt M (x, y) na niej (rys. 22). Wyznaczyć pola figur

a    o

krzywoliniowych A KM, OAM i OAML.

1

(') Można tu zrobić uwagę analogiczną do uwagi na str. 166, jednakże z powołaniem się na przykład

2

z ustępu 336.