0182

184

X. Zastosowania rachunku całkowego

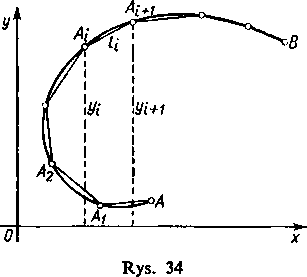
344. Pole powierzchni obrotowej. Przypuśćmy, że w płaszczyźnie xy (a dokładniej w górnej półpłaszczyźnie) dana jest pewna krzywa AB (rys. 34) o równaniach postaci (6), gdzie tp, y> są funkcjami ciągłymi, których pierwsze pochodne <p', y są również ciągłe. Przy założeniu, że na krzywej nie ma ani punktów osobliwych, ani wielokrotnych, możemy wprowadzić dla niej jako parametr łuk s, liczony od punktu A (/₀). Otrzymamy wtedy równania parametryczne postaci

(18)    x = #(s), y = V(s).

Parametr s zmienia się tu od 0 do S, gdzie S oznacza długość całej krzywej AB.

Przez obrót krzywej dokoła osi jc powstaje pewna powierzchnia obrotowa. Zadaniem naszym będzie obliczenie pola tej powierzchni.

Nie mamy możliwości zdefiniowania tu ogólnego pojęcia pola powierzchni zakrzywionej (tzn. niepłaskiej); zrobimy to w trzecim tomie. Obecnie zdefiniujemy to pojęcie tylko dla powierzchni obrotowych i nauczymy się obliczać pole takich powierzchni. Za punkt wyjścia dla tej definicji przyjmujemy znane ze szkoły reguły obliczania pól powierzchni bocznych walca, stożka i stożka ściętego. Później przekonamy się, że wzór, który otrzymamy teraz, jest szczególnym przypadkiem wzoru ogólnego na pole powierzchni zakrzywionej. Wybierzmy na krzywej AB w kierunku od A do B n+1 punktów (patrz rysunek 34)

(19)    Ao — A, Ai, A₂, ..., Ai, ..., A_n—i, A_n —- B

i rozpatrzmy łamaną A₀ A_t ... A_n__l B, wpisaną w krzywą. Wraz z krzywą obracamy dokoła osi x również tę łamaną; opisuje ona pewną powierzchnię, której pole umiemy znaleźć na podstawie wzorów z geometrii elementarnej. Przez pole powierzchni opisanej przez krzywą, będziemy rozumieli granicę pól \Q\ powierzchni opisywanych przez łamaną, przy założeniu, że długość najdłuższego odcinka łamanej dąży do 0. Ta definicja pola powierzchni obrotowej nasuwa nam metodę jego obliczania.

Wiemy już, że ciąg punktów (19) odpowiada rosnącemu ciągowi wartości parametru s, wstawionych między 0 i S:

0 — So < Si ^    < ... ^ Si < Si+i < ... < s_n~i ^ Sji — S.

Każde ogniwo łamanej przy obrocie dokoła osi x opisuje powierzchnię stożka ściętego (*). Jeśli oznaczymy rzędne punktów A_t i A_t+i odpowiednio przez y_t i y_l+1, a długość odcinka A_t A_t+i przez l_t, to pole powierzchni zakreślonej przez ten odcinek jest równe

i,.

₂„ Zi+Ziii

(!) w szczególności może to być powierzchnia walca lub stożka; jednakże i w tym przypadku jej pole dąje się wyznaczyć z ogólnego wzoru na pole powierzchni bocznej stożka ściętego.