0194

196

X. Zastosowania rachunku całkowego

prawa strona tego wzoru daje pole P powierzchni otrzymanej przez obrót krzywej AB [patrz 344, (20)], natomiast czynnik 2ntj po lewej stronie oznacza długość koła opisanego przez środek ciężkości krzywej przy jej obracaniu dokoła osi x, wreszcie 5 oznacza długość krzywej. Wobec tego możemy wypowiedzieć następujące twierdzenie Guldina:

Pole powierzchni otrzymanej przez obrót krzywej dokoła nieprzecinającej jej osi jest równe długości tej krzywej pomnożonej przez długość koła, opisanego przy tym przez środek ciężkości C krzywej (rys. 38)

|P| = Ul 2iri?.

Twierdzenie to pozwala znaleźć współrzędną t] środka ciężkości krzywej, jeśli znane są jej długości S i pole P powierzchni powstałej przez obrót tej krzywej dokoła danej osi.

• + 4t- = 1 względem osi x (przy założe-b

350. Przykłady. 1) Znaleźć moment statyczny elipsy -

niu, że a >b).

Moment statyczny górnej (lub dolnej) półelipsy różni się od pola odpowiedniej powierzchni obrotowej jedynie czynnikiem'2ir. Dlatego [patrz 345, 7)] jest

M_x = 2 b

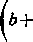
— arc sin e e

2) Jeśli rozpatrywana krzywa jest symetryczna względem pewnej prostej, to środek ciężkości tej krzywej leży zawsze na tej prostej.

Dla dowodu przyjmujemy, że osią symetrii jest oś y oraz że punkt przecięcia tej osi z krzywą jest początkiem liczenia długości łuku. Wtedy funkcja x = 0 (s) okazuje się funkcją nieparzystą zmiennej s i jeśli długość całej krzywej oznaczymy w tym przypadku przez 25, to otrzymamy [patrz 314, 9)]

s

My

j x ds = 0,

skąd wynika, że również f = 0.

3) Znaleźć na podstawie twierdzenia Guldina położenie środka ciężkości łuku AB (rys. 39) koła o promieniu r.

Ponieważ łuk ten jest symetryczny względem promienia OM przechodzącego przez środek łuku M, więc jego środek ciężkości C leży na tym promieniu, a zatem dla znalezienia położenia środka ciężkości

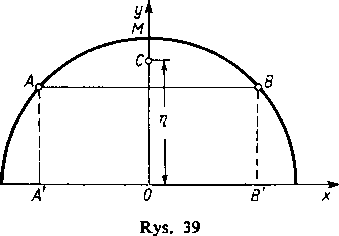
wystarczy znaleźć tylko jego odległość r] od środka O Wybieramy osie tak, jak wskazano na rysunku i oznaczamy długość łuku wAB przez s, a jego cięciwę AB (= A'B') — przez d. Przez obrót rozpatrywanego łuku dokoła osi x otrzymujemy część powierzchni kuli, której pole, jak wiemy, jest równe 2r.rd [345,1)]. Z twierdzenia Guldina wiemy natomiast, że to samo pole jest równe 2-kt\s, a więc

,    rd

stj = rd, rj = —.

i