0176

178

X. Zastosowania rachunku całkowego

płaszczyźnie xy krzywą o równaniu y = f(x) (a < x < b), gdzie funkcja/ (jc) jest nieujemną funkcją ciągłą. Obracając trapez krzywoliniowy ABCD, ograniczony z góry przez tę krzywą, dokoła osi x, otrzymamy bryłę V (rys. 28), która oczywiście podpada pod oma

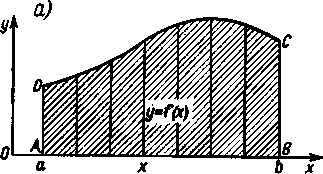
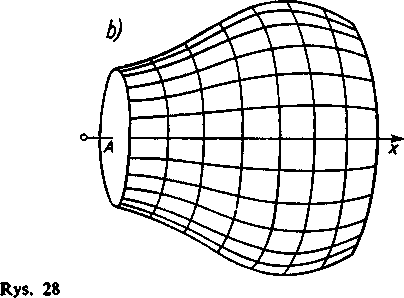
wiany przypadek, gdyż rzuty jej przekrojów na płaszczyznę prostopadłą do osi x są kołami współśrodkowymi. Mamy tu

\P(x)\ =ny² ««[/(x)F,

a więc (16)

Jeśli trapez krzywoliniowy jest ograniczony od dołu i z góry krzywymi y_t = f_t(x) i y₂ = fi(x), to jest oczywiście

6    b

\v\ = « / (y\-yl)dx = t:/ {[/atoP-LAOO]²} dx,

a    a

(17)

chociaż założenie o przekrojach może tu nie być spełnione. Udowodniony wynik łatwo jest rozciągnąć na wszystkie bryły powstające przez dodawanie lub odejmowanie brył, których przekroje spełniają wspomniany warunek.

Ogólnie prawdziwe jest jedynie następujące twierdzenie:

Jeśli bryła V ma objętość (¹), to objętość ta wyraża się wzorem (15).

Rzeczywiście, dla dowolnego e > 0 możemy między płaszczyznami x = a i x = b zbudować takie dwie bryły X* i Y*, złożone z równoległościanów, żeby pierwsza z nich leżała całkowicie wewnątrz bryły V, a druga zawierała V i żeby przy tym było Y* — X* < e. Ponieważ do tych brył można zastosować wzór (15), więc oznaczając przez | A (*)| i | B (x)| pola przekrojów tych brył otrzymujemy

b    b

\X*\=j\A(x)\dx,    |Y*| =/|B(x)|dx.

a    a

(‘) Tak będzie na przykład, jeśli bryła jest ograniczona jedną lub większą liczbą powierzchni gład kich [341].