0214

216

X. Zastosowania rachunku całkowego

Na odwrót, chcąc wyrazić 0 jako funkcją zmiennej t należy odwrócić funkcją

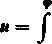
i |/l—*^Jsin²ą>

określoną całką eliptyczną. Z równości tej wynika, że p jest funkcją zmiennej ę monotonicznie rosnącą ciągłą (a także i różniczkowalną) w przedziale (— oo, + oo), która przyjmuje wartości również od — oo do + oo. Wobec tego [83] zmienna <p jest jednoznaczną funkcją zmiennej p w przedziale (— oo, + oo); Jacobi oznaczył ją symbolem am u (*). Z wzoru (16) mamy więc teraz

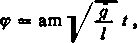
a zatem

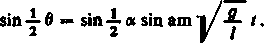
Funkcję sin am u (sinus amplitudy lub sinus eliptyczny) oznaczamy zazwyczaj krótko przez sn u (^ł). A więc ostatecznie zależność zmiennej 0 od ( wyraża się równością

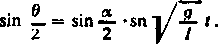
Na zakończenie wyznaczymy czas T jednego przejścia wahadła z położenia OB' do położenia OB; czas ten jest dwa razy większy od czasu potrzebnego na przejście wahadła od położenia O A do położenia OB. Podstawiając w (14) 0 = a lub w (15) <p = r./2 (³), otrzymujemy po podwojeniu T wyrażone przez całkę eliptyczną pierwszego rodzaju

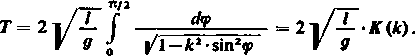
Zauważmy, że w rzeczywistości okres T wahań zależy od kąta « tzn. od wychylenia początkowego, ponieważ k zależy od «. Podstawiając — dla małych kątów — zamiast k zero otrzymujemy prosty wzór przybliżony

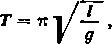
który też się zazwyczaj podaje w elementarnym kursie fizyki.

360. Uwagi o układaniu równań różniczkowych. Ograniczymy się do równań pierwszego rzędu postaci (8); rozpatrzymy zagadnienie układania takich równań. Proponujemy, aby czytelnik porównał nasze uwagi z tym, co mówiliśmy w ustępie 348 o prostszym równaniu

dQ- q (*) dx .

Z reguły przy układaniu równań trzeba rozpatrywać elementy nieskończenie małe omawianych figur i brył oraz nieskończenie małe przyrosty wielkości, o których mowa w zadaniu. Udało nam się co prawda uniknąć tego w poprzednim ustępie, ale tylko za cenę posługiwania się gotowym wyrażeniem na współczynnik kątowy stycznej, gotowymi wyrażeniami na prędkość zmiany tej, czy innej wielkości, które same wynikły z rozpatrywania elementów nieskończenie małych.

Przy układaniu zależności między nieskończenie małymi elementami należy posługiwać się wszystki-

(') am — są to początkowe litery słowa amplitudo (amplituda).

(^J) Funkcja sn u, rozpatrywana jako funkcja zmiennej zespolonej, jest jedną z najprostszych tzw. funkcji eliptycznych, wprowadzonych przez Abela i Jacobiego.

(³) Jeśli przyjąć, że górna granica całki (14) jest równa «, to całka ta jest „niewłaściwa” [patrz dalej 479], gdyż wtedy w przedziale całkowania funkcja podcałkowa jest nieograniczona. Trudności tej nie ma, jeśli posługujemy się całką (16).