0296

298

XI. Szeregi nieskończone o wyrazach stałych

także bezwzględnie zbieżny. Łącząc wyrazy z jednakowymi potęgami z, możemy go przekształcić w szereg iterowany

<p{x, z) = £/„(^{1 2})•²", (•)

•80

gdzie dla n > 0 jest

(-i)*

k\(k+n)l

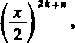
a dla n<0

C-D*

*!(*+»)!

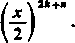
<P

Łatwo zresztą widać, że

J-n(x) = C-D"/„w •

Funkcja J. (x) (n = 0, 1, 2, ...) nazywa się funkcją Bessela o wskaźniku n. Funkcje te odgrywąją ważną rolę w fizyce matematycznej, mechanice nieba itd. Funkcja <p (x, z), z której rozwinięcia funkcje te się biorą, nazywa się funkcją generującą funkcje Bessela.

396. Szereg potęgowy dwóch zmiennych; obszar zbieżności. Szeregiem potęgowym dwóch zmiennych x, y nazywa się szereg podwójny postaci

(14)

t,

uporządkowany według całkowitych dodatnich potęg zmiennych x i y.

Tak jak to zrobiliśmy w 379 dla zwykłych szeregów potęgowych, postawimy sobie także i tutaj za zadanie zbadać kształt obszaru zbieżności szeregu (14), tzn. zbioru 9li = = {M (x, y)} tych punktów płaszczyzny, w których szereg ten jest zbieżny.

Lemat. Jeżeli szereg (14) jest zbieżny w pewnym punkcie M² (x², y²), którego obie współrzędne są różne od zera, to jest on bezwzględnie zbieżny we wszystkich punktach M(x,y) spełniających nierówności: |x| < |jc²|, |y| < |y²|, tzn. w całym otwartym prostokącie o środku w początku współrzędnych i wierzchołku M².

Dowód jest zupełnie analogiczny do dowodu lematu z ustępu 379. Z ograniczoności wyrazów szeregu (14) dla x = x², y = y²:

Wi.k x²‘y^2k| < L (/, k = 0, 1, 2, ...)

otrzymujemy

jeśli więc tylko |x| < |x²|, |y| < |y²|, to po prawej stronie mamy wyraz ogólny szeregu zbieżnego [396, 8)]. Stąd wynika bezwzględna zbieżność szeregu (16).

n-O

1

+CO

2

Suma a, jest z definicji sumą dwóch szeregów

—00

+ «    4-80