0631

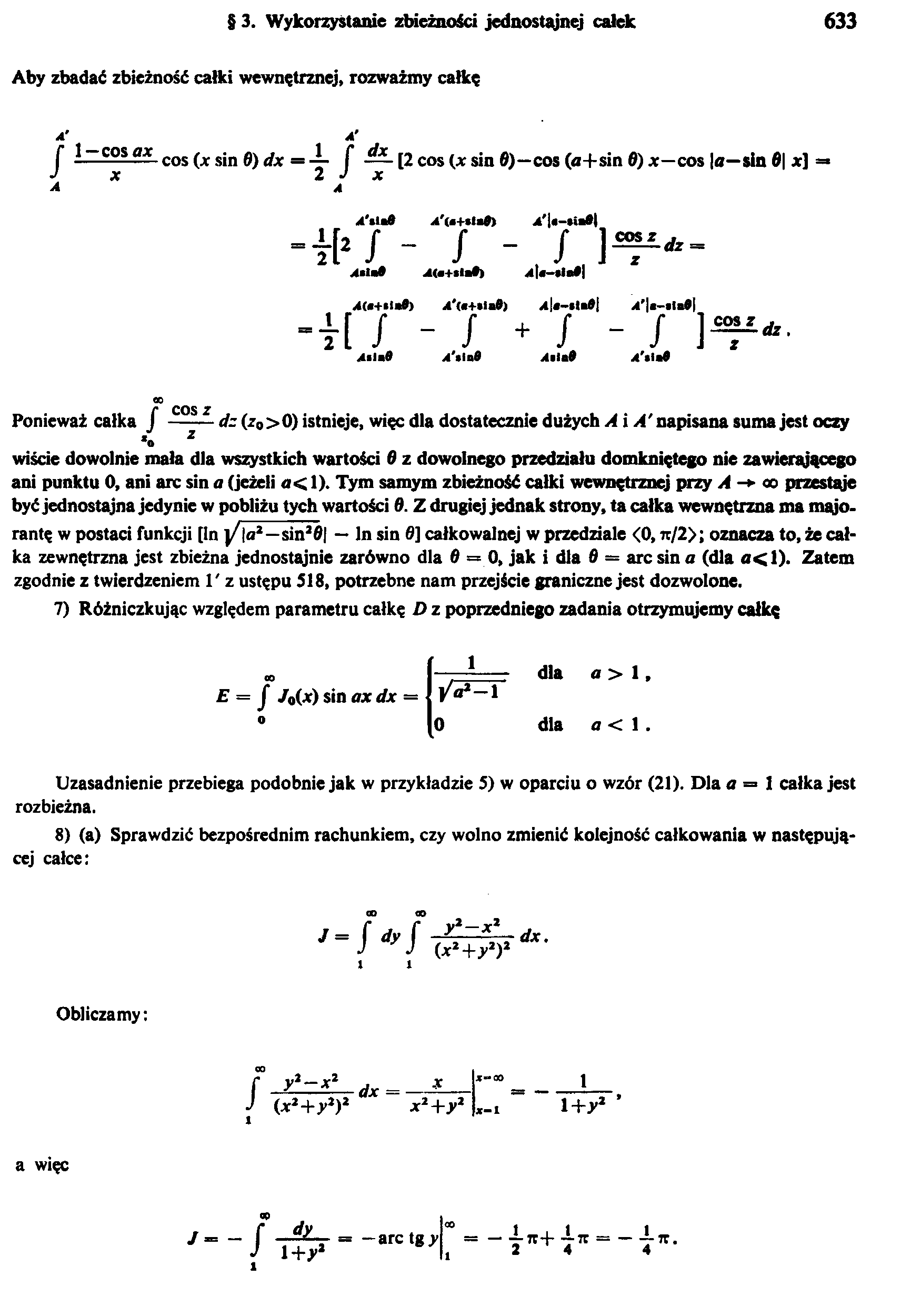
633

§ 3. Wykorzystanie zbieżności jednostajnej cdek

Aby zbadać zbieżność całki wewnętrznej, rozważmy całkę

f 1 ~ ^cos ax cos (_x sin 0) dx =

j    X

A

— f — [2 cos (x sin 0)—cos (a+sin 0) x—cos |o—sin 0| z] =»

2 J x

A

4W 4'(*+lil9)

W / - / -, /, ]***-

A» lw$    4<«łiial) 4|<-lltf|

4(«+ti*9)    4^#(«+Sia9)    a4|«-»l«0|    4'|«-«Ib0|

II / - / ⁺ / - / ]*?*■

4iii0    4'ilo0    4iia^    4'iiaf

/COS z

-d: (r_o>0) istnieje, więc dla dostatecznie dużych A i A 'napisana suma jest oczy

*o ^z

wiście dowolnie mała dla wszystkich wartości 0 z dowolnego przedziału domkniętego nie zawierającego ani punktu O, ani arc sin a (jeżeli a<l). Tym samym zbieżność całki wewnętrznej przy A -*■ oo przestaje być jednostajna jedynie w pobliżu tych wartości 0. Z drugiej jednak strony, ta całka wewnętrzna ma majo-rantę w postaci funkcji [ln j/|o²—sin²0| — ln sin 0] całkowalnej w przedziale <0, tr/2>; oznacza to, że całka zewnętrzna jest zbieżna jednostajnie zarówno dla 0 — 0, jak i dla 0 = arc sin a (dla a<l). Zatem zgodnie z twierdzeniem 1' z ustępu 518, potrzebne nam przejście graniczne jest dozwolone.

7) Różniczkując względem parametru całkę D z poprzedniego zadania otrzymujemy całkę

oo

E = j J<,(x) sin ax dx

1

l/a¹—1 0

dla    a > 1,

dla    a < 1.

Uzasadnienie przebiega podobnie jak w przykładzie 5) w oparciu o wzór (21). Dla a = 1 całka jest rozbieżna.

8) (a) Sprawdzić bezpośrednim rachunkiem, czy wolno zmienić kolejność całkowania w następującej całce:

dx.

J

f dyf

J J (*²+y²)²

i    i

Obliczamy:

dx =

f y¹-*²

J (*²+y²)²

x_l*"“

x²+y² Ui

1

1+y² *

a więc

J

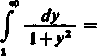
—arc tg y

1