24 luty 07 (59)

W równaniach (P3.126) występuje 6 niewiadomych: m_ki,m_k2,r_k1,r_k2,ę_k1,ę_k2. Przyjmujemy jako niewiadome momenty statyczne mas korekcyjnych: S₁ = m_kir_ki i S2 = ^mk2^rk2 ^oraz kąty <Pki< <Pk2' redukując w ten sposób liczbę niewiadomych do czterech. Rozwiązujemy układ równań (P3.126) otrzymując:

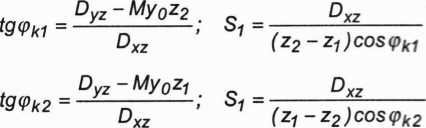
P3.127)

Przeprowadzone obliczenia wykazały, że wirnik można wyrównoważyć dynamicznie, umieszczając w dowolnie obranych płaszczyznach korekcyjnych n_1t n₂ dwie masy korekcyjne m_k1, m_k2 o momentach statycznych względem osi obrotu Oz równych S_?, S₂, pod kątami ę_k1, (p_k2. Istnieje oczywiście możliwość swobodnego doboru mas korekcyjnych i promieni ich zamocowania w takim zakresie, aby był spełniony warunek: S₍- = m_kir_ki dla / = 1; 2.

Przykład 3.21

Dany jest wał o masie M i środku ciężkości S leżącym na osi obrotu Oz wirujący wokół tej osi z prędkością kątową w (rys. 3.82), dla którego D xz ~ 0 ■ Dyz ~ 0-

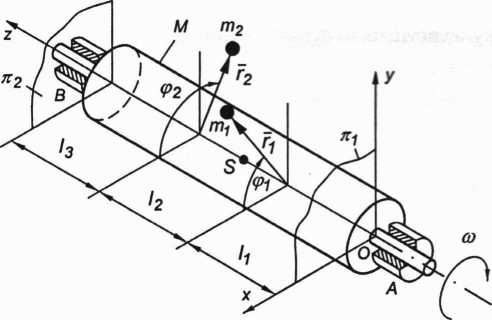
Rys. 3.82. Wyrównoważanie wału z układem mas skupionych

Niewyrównoważenie wału spowodowane jest układem dwóch mas m-j =10 g i m₂ = 20 g umieszczonych odpowiednio na promieniach r■, = 50 mm, r₂ = 40 mm, pod kątami = 60°, q>₂ = 120°, mierzonymi w układzie ruchomym Oxyz związanym z wałem. Dane są odległości: I-, =l₂ = l₃ = I = 200 mm. Położenie płaszczyzn korekcyjnych ji_1t n₂ jak na rysunku.

209