38 (311)

168

ODPOWIEDZI. WSKAZÓWKI. ROZWIĄZANIA

176.

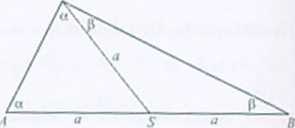
Rozwiązanie. Trójkąty ASC i SBC są równoramienne, więc mają równe kąty przv podstawie. \ZASC\= ISO" -2«. \ZBSC\ = 180°-2//.

\ZASC\+\ZJJSC\= I8t)’-2r» + ISO '-2/*= ISO'. Stąd a+fl=W>*\ćACH\_t więc trójkąt ABC jest prostokątny.

C

177. fi.

Rozwiązanie, n. b - długości pr/yprostokąlnych. c - długość przeciw prostokątnej. Wiemy, że a-rh= fi + fi -c i ab= I. <^:=«ł’+/i* - u, + /»)' -2ub = \(fi+fi)-c\^: 21 lfi+ fi)²-2-(fi + fi)c +« ’-2. Stąd 2<fi + fi)c = (fi t fi)²-2.

6 + 2^15 2fiifi + fi)

/.ilem <■ = = =- --=—

2{fi + fi\ 2tfi 4 fi)

fi.

178.

Rozwiązanie. iC/fj IR. gd/ie /< promień okręgu opisanego na trójkącie ABC. AKBS = AMS. więc |0| - \RL\ = r. XMSC a ,\SLC. więc |MC| - |/.C | = y. Zatcmz+y=2/?. U//|+|.1C| 2r+.i+y = 2r+2R.

179. a) y - ~_V_-T < *6(2;+®°).    180. l+sina+cosa

sinnr(I+tg yj

181. 45°.

Wskazówka. Skorzystaj ze związku między miarami kątów środkowego i wpisanego opartych na tym samym luku.

182. 0.6 lub 0.8.

183. j^h.

Rozwiązanie, u. b długości pr/yprostokąlnych. r - długość pr/cciwprostokątnej.

Wiemy, że <i+/» = 5A-e. Pole trójkąta: /' -0,5<r/> i /’ l),5Wi. stąd ab = eh.    i^;-₍r+/i'-i(i i-hr-Ztib (5h-c)^z-2di.

Równość (5/i-c)^:-2c/i =c^J sprowadzamy do postaci 25/r’=l2Wr. Starł c = -^j-h.

184. 3:10.

185. 30°. 60°. 90°.

Rozwiązanie. Trójkąt ASC jest równoramienny, więc |A'.Sl =    Odcinek CS zawiera się w

dwusiecznej kąta KCB. zatem    ^r -ę '•* twierdzenia o dwusircznej kąta trójkąta).

~ =    stąd 2n ftO®. Obliczenie miar kątów trójkąta jest tera/ natychmiastowe:

\ZACB\ = 3rr-90°. \ZKAC\ = W-rr-bO\ \ZKBC\ =90^J-2rr = 30".

C

186. fiia + b).

Wskazówka. Poprowadź dwusieczną lego kąta trójkąta, którego ramiona zawierają boki o długościach a i h. Uzasadnij, że dwusieczna ta dzieli dany trójkąta na dwa trójkąty. / których jeden jest równoramienny. a drugi jest podobny do danego.

187. 25:4.

188. 12:5.

190.

Gdy mc (0: I). to lg«-

V3trm-|)^J lm+3)(m-l)'

Gdy me (1; +•»). to tga=

73(m-t l)^:

(3mf lit ot-ll'

189. j.

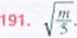
Wskazówka. Uzasadnij. Ze odległość punktu /' od boku AC jest równa -j | BC |. a <hI br*ku RC równa jest ±\AC |.

192. 5.7.9.