44 (283)

174_______________________ODPOWIEDZI. WSKAZÓWKI, ROZWIĄZANIA

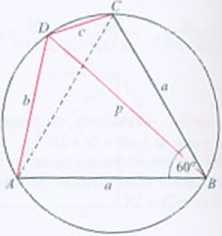
268.

Rozwiązanie. Trójkąt MIC jot równoboczny. więc IZ/MC1 = IZBCAI=60". 7. /te. o kątach wpisanych opartych na tym samym laku manty ',ZAl>H\ = 60" i I/.UDO = 00°. Y. tw. kosmosów dla trójkątów ADłł i BDC: a¹ = Ir + p^: - bp i a^: = c +/> -cp. Odejmując stronami oba równania, otrzymujemy bⁱ-c²-l>f> + cp=k). Stąd (6-o)(fc+c-/>j=0. Zatem h = c lub /•+<-=/».

Pokażemy, że równość h + c=p zachodzi także wtedy, gdy h - c. Jeśli h = c. to/; = l/ł/żl = -=-<j^3 (przekątna UD jest średnicą okr^u opisanego no trójkącie równobocznym ABC) i b = !A/żl = c =

- IDO = (.1/) i DC są hakami trójkąta równoramiennego o kącie ostrym 30"). Zatem

wtedy również, zachodzi równość b+c=p.

269. IBCI=4.

Rozwiązanie. Ozn. Itr - miara kąta DAB. Pola trójkątów. BCA i HCD mają równe pola. ponieważ. P_Bca Pbci + Pabf.> P«co - 1’tu t: + Pan-a wiemy, że Hem- Jeżeli pola trójkątów BCA i HCD mają równe p<>la, to wysokości obu trójkątów poprowadzone do boku UC uujątó’*-nc długości. Zatem punkty A i D są jednakowo odlegle od prostej BC. a to oznacza, że boki BC i Al) są równolegle. Jeżeli boki BC i Al) są równolegle, to IzI)AC\=\ZBCA\- er (bo kąty DAC i BCA są naprzemianlcgle, ii przekątna AC zawiera się w dwusiecznej kąta DAB). Zateta trójkąt ABC jest równoramienny (bo kąty przy wierzchołkach A i C mają miarę a), czyli boki AB i BC mają długość 4.

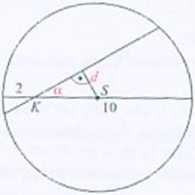
270. n.

271. 2.

Rozwiązanie, a = 30". Średnica okręgu ma długość 12, więc promień ma długość 6. IKSI=6-2=4. 4 = »in30" = 0.5. zatem d- 2.

272. 50” i litr.

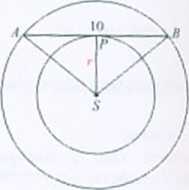
273. i 5f

Rozwiązanie. |a/’| = 5. I ASl = r c 3. Zf»v. Pitagorasa dla trójkąta PAS (r t 3)' = r > 5\ Stąd r- 24 Długość promienia większego okręgu jest równa 5-=-.

274. 4^34.

275. 12 cm¹.

Wskazówka. Jeśli <1 jest długością boku s/eściokąta foremnego, 10 długość promienia okręgu opisanego na tym sześeiokącie jest równa a. zaś długość promienia okręgu wpisanego równa jest długości wysokości trójkąta równobocznego o boku a.

276. a) 4; b) 4.

277.

3-73-zr

3y/3 +/r

278. Pole pierścienia: /’( v)=0.25n.i\ gd/ie .r-długość cięciwy AB. 279. 3.

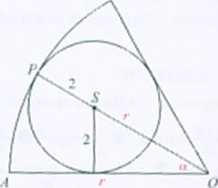
280. 6x.

Rozwiązanie. Środek S okręgu wpisanego w wycinek kola le/y na dwusiecznej kąta A OB, więc a = 3(1". | SO |=r - 2. ⁼ s>ⁿ30^l> = —. stąd r=6.

Obliczamy pole wycinka koła: -f- ■ x • 6* = brr.

281. 12 lub 2s/22.

282. I7n.

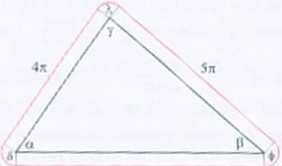
Rozwiązanie. ó= 360"-(90* + 90°+<i). <(>= 360°-(90* + W⁰ + fi),

A = 360'- (90"+90°+ył. d‘+ ę>+A'=5W^>-(a+0+ yt = 540°-180° = 360".

Zatem suma długości luków odpowiadających kątom śiodkowym d. ę. A jest równa długości okręgu o promieniu I.

Obliczamy długość linii: 2tt 1 +6n + 5n+4n = I7it